Question

If the sum of two smaller sides of a right – angled triangle is 17cm and the perimeter is 30cm, then find the area of the triangle.

Answer 1

The perimeter of the triangle = 30cm.
Let one of the two small sides = x
then, other side = 17 – x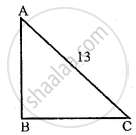

∴ Length of hypotenuse
= perimeter - sum of other two sides
= 30cm - 17cm 
= 13cm.
x² + (17 - x)² = (13)²  ...(Pythagoras theorem)
⇒ x² + 289 + x² - 34x = 169
⇒ 2x² - 34x + 289 - 169 = 0
⇒ 2x² - 34x + 120 = 0
⇒ x² - 17x + 60 = 0   ...(Dividing by 2)
⇒ x² - 12x - 5x + 60 = 0
⇒ x(x - 12) - 5(x - 12) = 0
⇒ (x - 12)(x - 5) = 0
Either x - 12 = 0,
then x = 12
or
x - 5 = 0,
then x = 5
(i) when x = 12, then first side = 12cm
and second side = 17 - 12 = 5cm
(ii) When x = 5, then first side = 5
and second side = 17 - 5 = 12
∴ Sides are 5cm. 12cm
Now, area of the triangle

= `(5 xx 12)/(2)`

= `(60)/(2)`
= 30cm².