Advertisements
Advertisements
प्रश्न
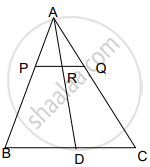
In ΔABC, P and Q are points on AB and AC, respectively, such that PQ is parallel to BC. Prove that the median AD drawn from A on BC bisects PQ.
योग
उत्तर
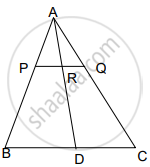
Suppose the median AD intersects PQ at R.
Given,
PQ || BC
or ∠APR = ∠B and ∠AQR = ∠C ...(Corresponding angles)
So in ΔAPR and ΔABD
∠APR = ∠ABD
∠PAR = ∠BAD
∴ ΔAPR ∼ ΔABD
or, `(PR)/(BD)` = `(AR)/(AD)` ....(i)
Similarly, ΔAQR ∼ ΔACD
or, `(QR)/(CD)` = `(AR)/(AD)` ....(ii)
From equation (i) and (ii),
`(PR)/(BD)` = `(QR)/(CD)`
or `(PR)/(BD)` = `(QR)/(CD)`, as CD = BD
or PR = QR
Hence, AD bisects PQ.
Hence proved.
shaalaa.com
क्या इस प्रश्न या उत्तर में कोई त्रुटि है?
