Advertisements
Advertisements
प्रश्न
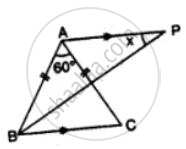
In Figure, BP bisects ∠ABC and AB = AC. Find x.
उत्तर
In the figure,
AB = AC, and BP bisects ∠ABC
AP || BC is drawn.
Now ∠PBC = ∠PBA .........(∵ PB is the bisector of ∠ABC)
∵ AP || BC
∴ ∠APB = ∠PBC ............(Alternate angles)
⇒ x = ∠PBC ..................(i)
In Δ ABC, ∠A = 60°
and ∠B = ∠C ...................(∵ AB = AC)
But ∠A + ∠B + ∠C = 180°.....................(Angles of a triangle)
⇒ 60° + ∠B + ∠C = 180°
⇒ 60° + ∠B + ∠B = 180°
⇒ 2 ∠B = 180° − 60° = 120°
∴ ∠B =`(120°)/2=60°`
⇒ `1/2∠"B"=(60°)/2=30°`
⇒ ∠PBC = 30°
∴ From (i),
x = 30°
APPEARS IN
संबंधित प्रश्न
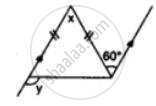
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
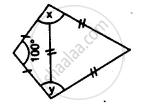
Find the unknown angles in the given figure:
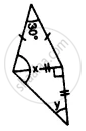
Apply the properties of isosceles and equilateral triangles to find the unknown angles in the given figure:
The vertical angle of an isosceles triangle is 15° more than each of its base angles. Find each angle of the triangle.
The ratio between a base angle and the vertical angle of an isosceles triangle is 1: 4. Find each angle of the triangle.
In the given figure, BI is the bisector of ∠ABC and Cl is the bisector of ∠ACB. Find ∠BIC.
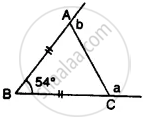
In ∆ ABC, BA and BC are produced. Find the angles a and h. if AB = BC.
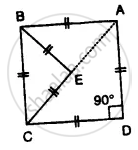
In the figure, given below, ABCD is a square, and ∆ BEC is an equilateral triangle. Find, the case:∠BAE
In the figure, AB is parallel to CD, find x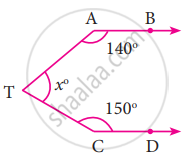
The angles of a triangle are in the ratio 1 : 2 : 3, find the measure of each angle of the triangle
