Advertisements
Advertisements
प्रश्न
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AE = ______ × AB.
उत्तर
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AE = 4 × AB.
Explanation:
∵ AB + BC + CD + DE = AE
⇒ AB + AB + AB + AB = AE
∴ 4 AB = AE
APPEARS IN
संबंधित प्रश्न
Number of lines passing through five points such that no three of them are collinear is ______.
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AD = AB + ______
Two angles can have exactly five points in common.
State the midpoints of all the sides of figure.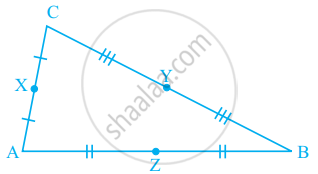
Look at a given figure. Mark a point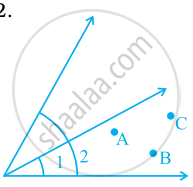
(a) A which is in the interior of both ∠1 and ∠2.
(b) B which is in the interior of only ∠1.
(c) Point C in the interior of ∠1.
Now, state whether points B and C lie in the interior of ∠2 also.
In given figure, is AB + AC = CB?
In given figure, is AB + BC = CA?
In the given, how many points are marked? Name them.
In the given figure, how many points are marked? Name them.
Draw a rough figure and label it suitably in the following case:
Point P lies on `overline"AB"`.
