Advertisements
Advertisements
Question
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AE = ______ × AB.
Solution
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AE = 4 × AB.
Explanation:
∵ AB + BC + CD + DE = AE
⇒ AB + AB + AB + AB = AE
∴ 4 AB = AE
APPEARS IN
RELATED QUESTIONS
Number of lines passing through five points such that no three of them are collinear is ______.
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AD = AC + ______
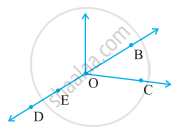
The number of common points in the two angles marked in figure ______.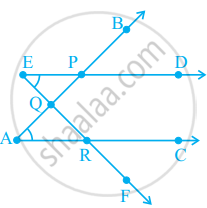
The number of common points in the two angles marked in figure is ______.
State the midpoints of all the sides of figure.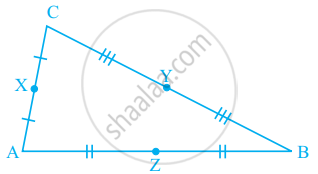
In given figure, is AB + AC = CB?
In given figure, is AB + BC = CA?
How many points are marked in the figure?
In the given, how many points are marked? Name them.
Use the figure to name Five points.