Advertisements
Advertisements
Question
Number of lines passing through five points such that no three of them are collinear is ______.
Options
10
5
20
8
Solution
Number of lines passing through five points such that no three of them are collinear is 10.
Explanation:
Since, total number of points is 5 and we need two points to form a line.
∴ Total number of lines passing through the points is 5 × 2 = 10
APPEARS IN
RELATED QUESTIONS
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Mid point of AE is ______
The number of common points in the two angles marked in figure is ______.
Look at a given figure. Mark a point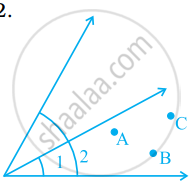
(a) A which is in the interior of both ∠1 and ∠2.
(b) B which is in the interior of only ∠1.
(c) Point C in the interior of ∠1.
Now, state whether points B and C lie in the interior of ∠2 also.
In given figure, is AC + CB = AB ?
In given figure, is AB + AC = CB?
In given figure, is AB + BC = CA?
In the given, how many points are marked? Name them.
In given figure, how many points are marked? Name them.
Use the figure to name Five points.
Consider the following figure of line \[\overleftrightarrow{MN}\]. Say whether the following statement is true or false in the context of the given figure.
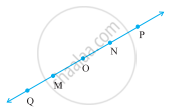
N is the initial point of `vec("NP")` and `vec("NM")`.
