Advertisements
Advertisements
Question
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Midpoint of CE is ______
Solution
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Midpoint of CE is D
Explanation:
∵ CD = DE
APPEARS IN
RELATED QUESTIONS
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AD = AB + ______
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AD = AC + ______
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Mid point of AE is ______
Two angles can have exactly five points in common.
Look at a given figure. Mark a point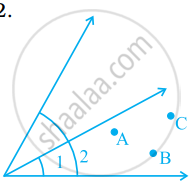
(a) A which is in the interior of both ∠1 and ∠2.
(b) B which is in the interior of only ∠1.
(c) Point C in the interior of ∠1.
Now, state whether points B and C lie in the interior of ∠2 also.
In given figure, is AC + CB = AB ?
In given figure, is AB + AC = CB?
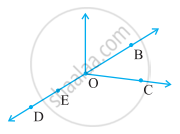
In given figure, how many points are marked? Name them.
Use the figure to name Five points.
Draw a rough figure and label it suitably in the following case:
Point P lies on `overline"AB"`.
