Advertisements
Advertisements
Question
Two angles can have exactly five points in common.
Options
True
False
Solution
This statement is False.
Explanation:
∵ It can have any number of points.
APPEARS IN
RELATED QUESTIONS
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AE = ______ × AB.
The number of common points in the two angles marked in figure ______.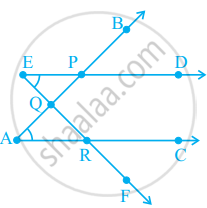
The number of common points in the two angles marked in figure is ______.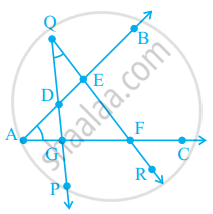
State the midpoints of all the sides of figure.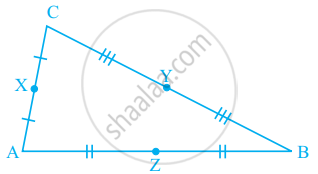
In given figure, is AB + BC = CA?
How many points are marked in the figure?
In the given figure, how many points are marked? Name them.
In given figure, how many points are marked? Name them.
Consider the following figure of line \[\overleftrightarrow{MN}\]. Say whether the following statement is true or false in the context of the given figure.
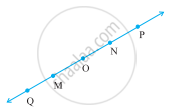
O is not an initial point of `vec("OP")`.
Consider the following figure of line \[\overleftrightarrow{MN}\]. Say whether the following statement is true or false in the context of the given figure.

N is the initial point of `vec("NP")` and `vec("NM")`.
