Advertisements
Advertisements
Question
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AD = AB + ______
Solution
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then
AD = AB + BD
Explanation:
BD: AD = AB + BC + CD = AB + BD
APPEARS IN
RELATED QUESTIONS
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Mid point of AE is ______
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
Midpoint of CE is ______
In figure, points A, B, C, D and E are collinear such that AB = BC = CD = DE. Then 
AE = ______ × AB.
Two angles can have exactly five points in common.
State the midpoints of all the sides of figure.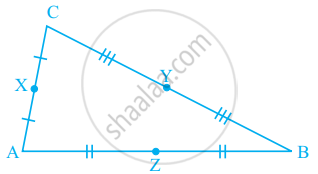
In given figure, is AC + CB = AB ?
How many points are marked in the figure?
In the given figure, how many points are marked? Name them.
Draw a rough figure and label it suitably in the following case:
Point P lies on `overline"AB"`.
Consider the following figure of line \[\overleftrightarrow{MN}\]. Say whether the following statement is true or false in the context of the given figure.
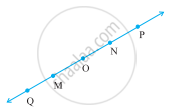
O is not an initial point of `vec("OP")`.
