Advertisements
Advertisements
प्रश्न
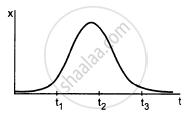
In figure shows the x coordinate of a particle as a function of time. Find the sings of vx and ax at t = t1, t = t2 and t = t3.
उत्तर
The slope of the x–t graph gives the velocity, and the change in the slope gives the acceleration.
At t = t1,
Slope = Positive ⇒ Velocity = Positive
The slope is increasing ⇒ Acceleration = Positive
At t = t2,
Slope = Constant ⇒ Velocity = Zero
The slope is constant ⇒ Acceleration = Negative
At t = t3,
Slope = Negative ⇒ Velocity = Negative
The slope is increasing ⇒ Acceleration = Positive
APPEARS IN
संबंधित प्रश्न
Suggest a suitable physical situation for the following graph:
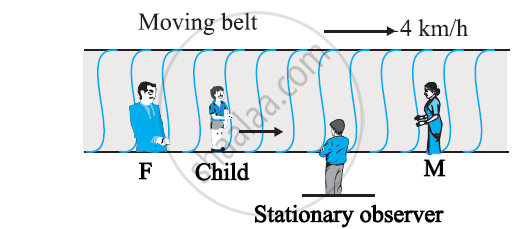
On a long horizontally moving belt (Fig. 3.26), a child runs to and fro with a speed 9 km h–1 (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km h–1. For an observer on a stationary platform outside, what is the
(a) speed of the child running in the direction of motion of the belt ?.
(b) speed of the child running opposite to the direction of motion of the belt ?
(c) time taken by the child in (a) and (b) ?
Which of the answers alter if motion is viewed by one of the parents?
Give example where the velocity of a particle is zero but its acceleration is not zero.
Give example where the velocity is opposite in direction to the acceleration.
Give example where the velocity is perpendicular to the acceleration.
The accelerations of a particle as seen from two frames S1 and S2 have equal magnitude 4 m/s2.
The displacement of particle is given by x = `2/lambda (1 - e^(-lambdat))`, the acceleration of particle at 2s when λ = 2s–1 will be (Take `l`n 0.018 = – 4)
If the velocity of a car is given by V = (150 − 10x)½ m/s. If a car retards their motion by applying brakes then what will be the acceleration?
A lift is coming from 8th floor and is just about to reach 4th floor. Taking ground floor as origin and positive direction upwards for all quantities, which one of the following is correct?
A graph of x versus t is shown in figure. Choose correct alternatives from below.
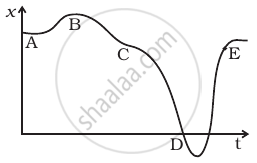
- The particle was released from rest at t = 0.
- At B, the acceleration a > 0.
- At C, the velocity and the acceleration vanish.
- Average velocity for the motion between A and D is positive.
- The speed at D exceeds that at E.
Give example of a motion where x > 0, v < 0, a > 0 at a particular instant.
An object falling through a fluid is observed to have acceleration given by a = g – bv where g = gravitational acceleration and b is constant. After a long time of release, it is observed to fall with constant speed. What must be the value of constant speed?
