Advertisements
Advertisements
प्रश्न
In figure shows the x coordinate of a particle as a function of time. Find the sings of vx and ax at t = t1, t = t2 and t = t3.
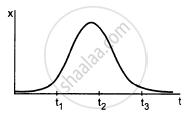
उत्तर
The slope of the x–t graph gives the velocity, and the change in the slope gives the acceleration.
At t = t1,
Slope = Positive ⇒ Velocity = Positive
The slope is increasing ⇒ Acceleration = Positive
At t = t2,
Slope = Constant ⇒ Velocity = Zero
The slope is constant ⇒ Acceleration = Negative
At t = t3,
Slope = Negative ⇒ Velocity = Negative
The slope is increasing ⇒ Acceleration = Positive
APPEARS IN
संबंधित प्रश्न
Read the statement below carefully and state, with reason and example, if it is true or false:
A particle in one-dimensional motion with constant speed must have zero acceleration.
Read the statement below carefully and state, with reason and example, if it is true or false:
A particle in one-dimensional motion with positive value of acceleration must be speeding up.
Suggest a suitable physical situation for the following graph:
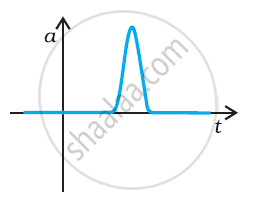
The given figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D?

If a particle is accelerating, it is either speeding up or speeding down. Do you agree with this statement?
Give example where the velocity is opposite in direction to the acceleration.
Give example where the velocity is perpendicular to the acceleration.
A stone is released from an elevator going up with an acceleration a. The acceleration of the stone after the release is
The accelerations of a particle as seen from two frames S1 and S2 have equal magnitude 4 m/s2.
The displacement of particle is given by x = `2/lambda (1 - e^(-lambdat))`, the acceleration of particle at 2s when λ = 2s–1 will be (Take `l`n 0.018 = – 4)
If the velocity of a car is given by V = (150 − 10x)½ m/s. If a car retards their motion by applying brakes then what will be the acceleration?
A graph of x versus t is shown in figure. Choose correct alternatives from below.
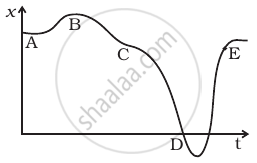
- The particle was released from rest at t = 0.
- At B, the acceleration a > 0.
- At C, the velocity and the acceleration vanish.
- Average velocity for the motion between A and D is positive.
- The speed at D exceeds that at E.
Give example of a motion where x > 0, v < 0, a > 0 at a particular instant.
