Advertisements
Advertisements
प्रश्न
Give example of a motion where x > 0, v < 0, a > 0 at a particular instant.
उत्तर
Let the motion is represented by `x(t) = A + Be^(-γt)` .....(i)
Let A > B and ϒ > 0
Now velocity `x(t) = (dx)/(dt) = - Bγ^(-γt)`
Acceleration `a(t) = (dx)/(dt) = Bγ^2e^(-γt)`
Suppose we are considering any instant t, then from equation (i), we can say that
x(t) > 0; v(t) < 0 and a > 0
APPEARS IN
संबंधित प्रश्न
Read the statement below carefully and state, with reason and example, if it is true or false:
A particle in one-dimensional motion with constant speed must have zero acceleration.
Read the statement below carefully and state, with reason and example, if it is true or false:
A particle in one-dimensional motion with positive value of acceleration must be speeding up.
Suggest a suitable physical situation for the following graph:
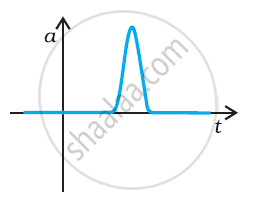
The given figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D?

Give example where the velocity of a particle is zero but its acceleration is not zero.
Give example where the velocity is opposite in direction to the acceleration.
Give example where the velocity is perpendicular to the acceleration.
An object having a velocity 4.0 m/s is accelerated at the rate of 1.2 m/s2 for 5.0 s. Find the distance travelled during the period of acceleration.
A lift is coming from 8th floor and is just about to reach 4th floor. Taking ground floor as origin and positive direction upwards for all quantities, which one of the following is correct?
A graph of x versus t is shown in figure. Choose correct alternatives from below.
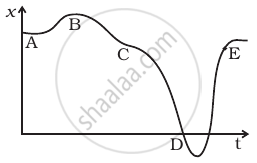
- The particle was released from rest at t = 0.
- At B, the acceleration a > 0.
- At C, the velocity and the acceleration vanish.
- Average velocity for the motion between A and D is positive.
- The speed at D exceeds that at E.
