Advertisements
Advertisements
प्रश्न
An object falling through a fluid is observed to have acceleration given by a = g – bv where g = gravitational acceleration and b is constant. After a long time of release, it is observed to fall with constant speed. What must be the value of constant speed?
उत्तर
When speed becomes constant acceleration a = `(dv)/(dt)` = 0
Given acceleration a = g – bv
Where, g = gravitational acceleration
Clearly, from the above equation as speed increases acceleration will decrease. At a certain speed say v0, acceleration will be zero and speed will remain constant.
Hence, a = g – bv0 = 0
⇒ v0 = g/b
APPEARS IN
संबंधित प्रश्न
Suggest a suitable physical situation for the following graph:
The given figure gives a speed-time graph of a particle in motion along a constant direction. Three equal intervals of time are shown. In which interval is the average acceleration greatest in magnitude? In which interval is the average speed greatest? Choosing the positive direction as the constant direction of motion, give the signs of v and a in the three intervals. What are the accelerations at the points A, B, C and D?

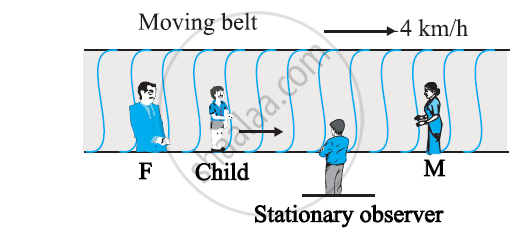
On a long horizontally moving belt (Fig. 3.26), a child runs to and fro with a speed 9 km h–1 (with respect to the belt) between his father and mother located 50 m apart on the moving belt. The belt moves with a speed of 4 km h–1. For an observer on a stationary platform outside, what is the
(a) speed of the child running in the direction of motion of the belt ?.
(b) speed of the child running opposite to the direction of motion of the belt ?
(c) time taken by the child in (a) and (b) ?
Which of the answers alter if motion is viewed by one of the parents?
Give example where the velocity of a particle is zero but its acceleration is not zero.
Give example where the velocity is opposite in direction to the acceleration.
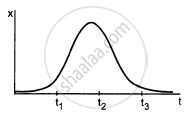
In figure shows the x coordinate of a particle as a function of time. Find the sings of vx and ax at t = t1, t = t2 and t = t3.
The accelerations of a particle as seen from two frames S1 and S2 have equal magnitude 4 m/s2.
The displacement of particle is given by x = `2/lambda (1 - e^(-lambdat))`, the acceleration of particle at 2s when λ = 2s–1 will be (Take `l`n 0.018 = – 4)
A graph of x versus t is shown in figure. Choose correct alternatives from below.
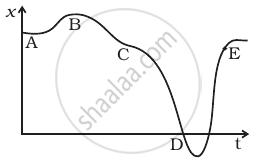
- The particle was released from rest at t = 0.
- At B, the acceleration a > 0.
- At C, the velocity and the acceleration vanish.
- Average velocity for the motion between A and D is positive.
- The speed at D exceeds that at E.
Give example of a motion where x > 0, v < 0, a > 0 at a particular instant.
