Advertisements
Advertisements
प्रश्न
In the given figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r2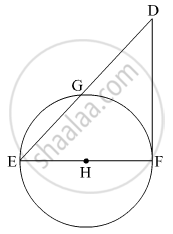
उत्तर
Given
In the given figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r.
To prove, DE × GE = 4r2
seg DF ⊥ seg HF
∴ ∠HFD = 90º ...(Tangent at any point of a circle is perpendicular to the radius through the point of contact)
Using the tangent secant segments theorem, we have
DF2 = DE × DG .....(1)
Now, In Δ DFE, ∠F = 90º
By Pythagoras theorem,
DE2 = DF2 + EF2
DE2 = DE × DG + 2r2 ...(From eqn (1) and diameter = 2 × radius)
DE2 = DE × DG + 4r2
DE2 − DE × DG = 4r2
DE × (DE − DG) = 4r2
DE × GE = 4r2 ...(D - G - E)
Hence, DE × GE = 4r2
APPEARS IN
संबंधित प्रश्न
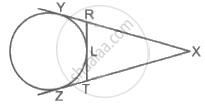
In the adjoining figure, O is the centre of the circle. From point R, seg RM and seg RN are tangent segments touching the circle at M and N. If (OR) = 10 cm and radius of the circle = 5 cm, then
- What is the length of each tangent segment?
- What is the measure of ∠MRO?
- What is the measure of ∠MRN?

Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity.
In the given figure, the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm. 
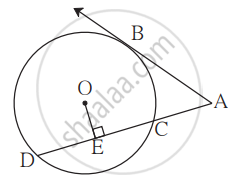
In the given figure, O is the centre of the circle and B is a point of contact. seg OE ⊥ seg AD, AB = 12, AC = 8, find (1) AD (2) DC (3) DE.
In the given figure, M is the centre of the circle and seg KL is a tangent segment.
If MK = 12, KL = \[6\sqrt{3}\] then find –
(1) Radius of the circle.
(2) Measures of ∠K and ∠M.
In the given figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r, Prove that ▢ABOC is a square. 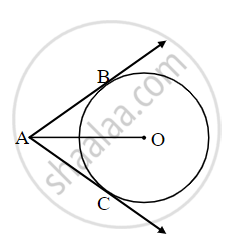
Proof: Draw segment OB and OC.
l(AB) = r ......[Given] (I)
AB = AC ......[`square`] (II)
But OB = OC = r ......[`square`] (III)
From (i), (ii) and (iii)
AB = `square` = OB = OC = r
∴ Quadrilateral ABOC is `square`
Similarly, ∠OBA = `square` ......[Tangent Theorem]
If one angle of `square` is right angle, then it is a square.
∴ Quadrilateral ABOC is a square.
In the following figure ‘O’ is the centre of the circle.
∠AOB = 1100, m(arc AC) = 450.
Use the information and fill in the boxes with proper numbers.
(i) m(arcAXB) =
(ii)m(arcCAB) =
(iv)∠COB =
(iv)m(arcAYB) =
Prove the following theorem:
Tangent segments drawn from an external point to the circle are congruent.
Segment DP and segment DQ are tangent segments to the circle with center A. If DP = 7 cm. So find the length of the segment DQ.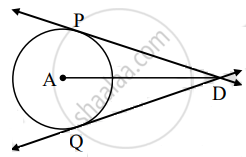
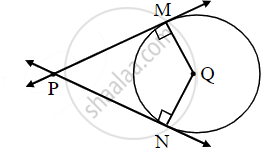
In the adjoining figure circle with Centre, Q touches the sides of ∠MPN at M and N. If ∠MPN = 40°, find measure of ∠MQN.
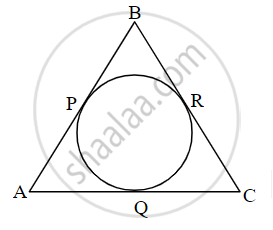
The figure ΔABC is an isosceles triangle with a perimeter of 44 cm. The sides AB and BC are congruent and the length of the base AC is 12 cm. If a circle touches all three sides as shown in the figure, then find the length of the tangent segment drawn to the circle from point B.
If AB and CD are the common tangents in the circles of two unequal (different) radii, then show that seg AB ≅ seg CD.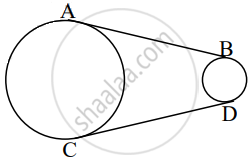
Seg RM and seg RN are tangent segments of a circle with centre O. Prove that seg OR bisects ∠MRN as well as ∠MON with the help of activity.

Proof: In ∆RMO and ∆RNO,
∠RMO ≅ ∠RNO = 90° ......[`square`]
hypt OR ≅ hypt OR ......[`square`]
seg OM ≅ seg `square` ......[Radii of the same circle]
∴ ∆RMO ≅ ∆RNO ......[`square`]
∠MOR ≅ ∠NOR
Similairy ∠MRO ≅ `square` ......[`square`]
In a parallelogram ABCD, ∠B = 105°. Determine the measure of ∠A and ∠D.
In the following figure, XY = 10 cm and LT = 4 cm. Find the length of XT.