Advertisements
Advertisements
प्रश्न
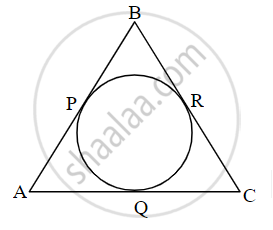
The figure ΔABC is an isosceles triangle with a perimeter of 44 cm. The sides AB and BC are congruent and the length of the base AC is 12 cm. If a circle touches all three sides as shown in the figure, then find the length of the tangent segment drawn to the circle from point B.
उत्तर
Given: AB + BC + AC = 44 cm
AC = 12 cm
To find: l(BP) , l(BR)
Solution:
`{:("seg AP" ≅ "seg AQ"),("seg QC" ≅ "seg RC"),("seg BP" ≅ "seg BR"):}}` .......[Tangent Segment theorem]
`{:("Let" l("AP") = l("AQ") = x","),(l("QC") = l("RC") = y","),(l("BP") = l("BR") = "z"):}}` .....(i)
AC = AQ + QC ......[A – Q – C]
∴ AC = x + y
∴ x + y = 12 ......(ii) [Given]
AB + BC + AC = 44 ......[Given]
∴ (AP + PB) + (BR + RC) + (AQ + QC) = 44 ......[A–P–B, B–R–C, A–Q–C]
∴ x + z + z + y + x + y = 44 ......[From (i)]
∴ 2x + 2y + 2z = 44
∴ 2(x + y) + 2z = 44
∴ 2(12) + 2z = 44 ......[From (ii)]
∴ 24 + 2z = 44
∴ 2z = 44 – 24
∴ 2z = 20
∴ z = 10 ......(iiii)
∴ l(BP) = l(BR) = 10 cm ......[From (i) and (iii)]
APPEARS IN
संबंधित प्रश्न
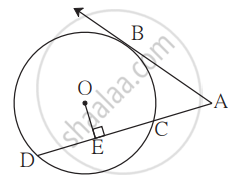
In the given figure, the circles with centres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD if the radii of the circles are 4 cm, 6 cm. 
In the given figure, O is the centre of the circle and B is a point of contact. seg OE ⊥ seg AD, AB = 12, AC = 8, find (1) AD (2) DC (3) DE.
In the given figure, seg EF is a diameter and seg DF is a tangent segment. The radius of the circle is r. Prove that, DE × GE = 4r2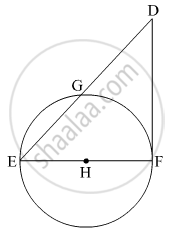
Four alternative answers for the following question is given. Choose the correct alternative.
Length of a tangent segment drawn from a point which is at a distance 12.5 cm from the centre of a circle is 12 cm, find the diameter of the circle.
Four alternative answers for the following question is given. Choose the correct alternative.
Seg XZ is a diameter of a circle. Point Y lies in its interior. How many of the following statements are true ? (i) It is not possible that ∠XYZ is an acute angle. (ii) ∠XYZ can’t be a right angle. (iii) ∠XYZ is an obtuse angle. (iv) Can’t make a definite statement for measure of ∠XYZ.
In the given figure, O is the centre of the circle. Seg AB, seg AC are tangent segments. Radius of the circle is r and l(AB) = r, Prove that ▢ABOC is a square. 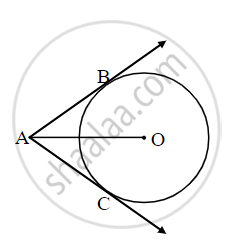
Proof: Draw segment OB and OC.
l(AB) = r ......[Given] (I)
AB = AC ......[`square`] (II)
But OB = OC = r ......[`square`] (III)
From (i), (ii) and (iii)
AB = `square` = OB = OC = r
∴ Quadrilateral ABOC is `square`
Similarly, ∠OBA = `square` ......[Tangent Theorem]
If one angle of `square` is right angle, then it is a square.
∴ Quadrilateral ABOC is a square.
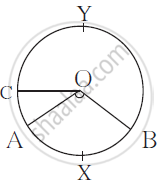
In the following figure ‘O’ is the centre of the circle.
∠AOB = 1100, m(arc AC) = 450.
Use the information and fill in the boxes with proper numbers.
(i) m(arcAXB) =
(ii)m(arcCAB) =
(iv)∠COB =
(iv)m(arcAYB) =
The perpendicular height of a cone is 12 cm and its slant height is 13 cm. Find the radius of the base of the cone.
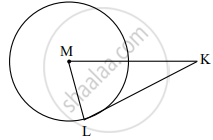
In the given figure, M is the centre of the circle and seg KL is a tangent segment. L is a point of contact. If MK = 12, KL = `6sqrt3`, then find the radius of the circle.
Prove the following theorem:
Tangent segments drawn from an external point to the circle are congruent.
Length of a tangent segment drawn from a point which is at a distance 15 cm from the centre of a circle is 12 cm, find the diameter of the circle?
Tangent segments drawn from an external point to a circle are congruent, prove this theorem. Complete the following activity.
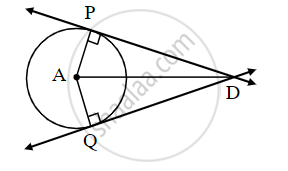
Given: `square`
To Prove: `square`
Proof: Draw radius AP and radius AQ and complete the following proof of the theorem.
In ∆PAD and ∆QAD,
seg PA ≅ `square` .....[Radii of the same circle]
seg AD ≅ seg AD ......[`square`]
∠APD ≅ ∠AQD = 90° .....[Tangent theorem]
∴ ∆PAD ≅ ∆QAD ....[`square`]
∴ seg DP ≅ seg DQ .....[`square`]
If AB and CD are the common tangents in the circles of two unequal (different) radii, then show that seg AB ≅ seg CD.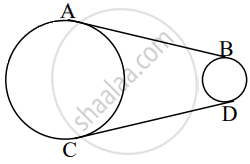
Prove that, tangent segments drawn from an external point to the circle are congruent.

A circle touches side BC at point P of the ΔABC, from outside of the triangle. Further extended lines AC and AB are tangents to the circle at N and M respectively. Prove that : AM = `1/2` (Perimeter of ΔABC)
