Advertisements
Advertisements
प्रश्न
In rectangle OABC; point O is the origin, OA = 10 units along x-axis and AB = 8 units. Find the co-ordinates of vertices A, B and C.
उत्तर
Given that in rectangle OABC; point O is the origin and OA = 10 units along x-axis therefore we get O(0,0) and A(0,0). Also it is given that AB = 8 units. Therefore we get B(10,8) and C(0,8)
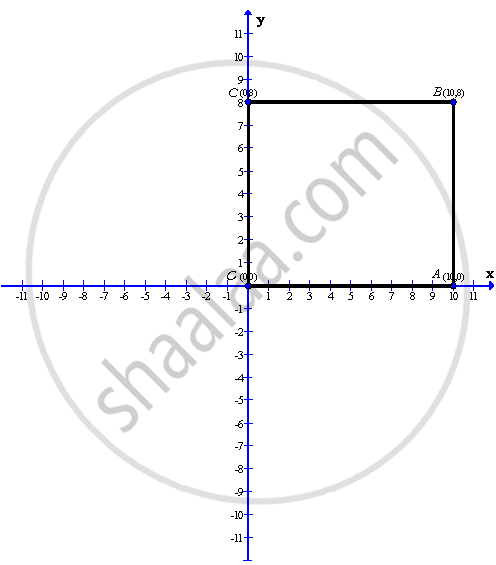
After plotting the points O(0,0), A(10,0), B(10,8) and C(0,8) on a graph paper; we get the above rectangle OABC and the required co-ordinates of the vertices are A(10,0), B(10,8) and C(0,8)
APPEARS IN
संबंधित प्रश्न
Find the values of x and y if:
(3x + 1, 2y - 7) = (9, - 9)
State, true or false:
The y-axis is the vertical number line.
State, true or false:
The point (a, b) lies on the y-axis if b = 0.
In the following, find the coordinates of the point whose abscissa is the solution of the first equation and ordinate is the solution of the second equation:
3 - 2x = 7; 2y + 1 = 10 - 2`(1)/(2)`y.
Find the co-ordinates of points whose: Abscissa is 6 and ordinate is 2
Find the co-ordinates of points whose: Abscissa is -2 and ordinate is 0
Find the co-ordinates of points whose: Abscissa is -7 and ordinate is 4
In each of the following, find the coordinates of the point whose abscissa is the solution of the first equation and ordinate is the solution of the second equation.
(7 - x) + 7x = `(x + 5); (2 + 3y)/(2)` = 2y - 6
The x-coordinate is always ______ on the y-axis
(−9, 0) lies on the x-axis
