Advertisements
Advertisements
प्रश्न
In the figure, the centre of the circle is O and ∠STP = 40°.
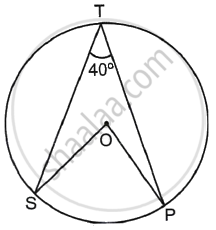
- m (arc SP) = ? By which theorem?
- m ∠SOP = ? Give reason.
उत्तर
Given: ∠STP = 40°
i. m(arc SP) = 2∠STP
⇒ m(arc SP) = 2 × 40° = 80°
Hence, m(arc SP) is 80° by inscribed angle theorem.
ii. m∠SOP = 2 × m∠STP
= 2 × 40° = 80°
As a result, m∠SOP is 80° since the angle subtended by an arc at the centre of the circle is twice the angle subtended by the arc at any point on the circle.
APPEARS IN
संबंधित प्रश्न
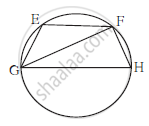
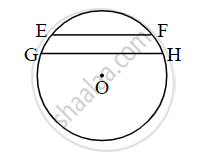
In the adjoining figure chord EF || chord GH.
Prove that chord EG ≅ chord FH.
Fill in the boxes and write the complete proof.
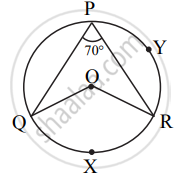
In the given figure, O is the centre of the circle, ∠QPR = 70° and m(arc PYR) = 160°, then find the value of the following m(arc QXR).
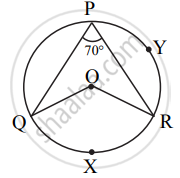
In the given figure, O is centre of circle. ∠QPR = 70° and m(arc PYR) = 160°, then find the value of the following ∠QOR.
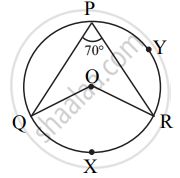
In the given figure, O is centre of circle, ∠QPR = 70° and m(arc PYR) = 160°, then find the value of the following ∠PQR.

A circle with centre P is inscribed in the ABC. Side AB, side BC and side AC touch the circle at points L, M and N respectively. Radius of the circle is r.
Prove that: `"A" (triangle "ABC") =1/2 ("AB" + "BC" + "AC") xx "r"`
In the figure, if the chord PQ and chord RS intersect at point T, prove that: m∠STQ = `1/2` [m(arc PR) + m(arc SQ)] for any measure of ∠STQ by filling out the boxes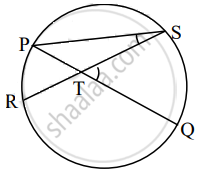
Proof: m∠STQ = m∠SPQ + `square` .....[Theorem of the external angle of a triangle]
= `1/2` m(arc SQ) + `square` .....[Inscribed angle theorem]
= `1/2 [square + square]`
In figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.
Proof: Draw seg GF.
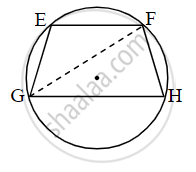
∠EFG = ∠FGH ......`square` .....(I)
∠EFG = `square` ......[inscribed angle theorem] (II)
∠FGH = `square` ......[inscribed angle theorem] (III)
∴ m(arc EG) = `square` ......[By (I), (II), and (III)]
chord EG ≅ chord FH ........[corresponding chords of congruent arcs]
The angle inscribed in the semicircle is a right angle. Prove the result by completing the following activity.

Given: ∠ABC is inscribed angle in a semicircle with center M
To prove: ∠ABC is a right angle.
Proof: Segment AC is a diameter of the circle.
∴ m(arc AXC) = `square`
Arc AXC is intercepted by the inscribed angle ∠ABC
∠ABC = `square` ......[Inscribed angle theorem]
= `1/2 xx square`
∴ m∠ABC = `square`
∴ ∠ABC is a right angle.
Prove that angles inscribed in the same arc are congruent.
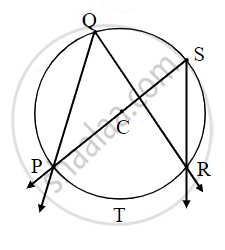
Given: In a circle with center C, ∠PQR and ∠PSR are inscribed in same arc PQR. Arc PTR is intercepted by the angles.
To prove: ∠PQR ≅ ∠PSR.
Proof:
m∠PQR = `1/2 xx ["m"("arc PTR")]` ......(i) `square`
m∠`square` = `1/2 xx ["m"("arc PTR")]` ......(ii) `square`
m∠`square` = m∠PSR .....[By (i) and (ii)]
∴ ∠PQR ≅ ∠PSR
In the figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that, seg AD ≅ seg BD. Complete the following proof by filling in the blanks.
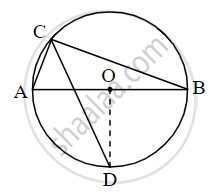
Proof:
Draw seg OD.
∠ACB = `square` ......[Angle inscribed in semicircle]
∠DCB = `square` ......[CD is the bisector of ∠C]
m(arc DB) = `square` ......[Inscribed angle theorem]
∠DOB = `square` ......[Definition of measure of an arc](i)
seg OA ≅ seg OB ...... `square` (ii)
∴ Line OD is `square` of seg AB ......[From (i) and (ii)]
∴ seg AD ≅ seg BD
In the figure, chord LM ≅ chord LN, ∠L = 35°.

Find
(i) m(arc MN)
(ii) m(arc LN)
In the figure, if O is the center of the circle and two chords of the circle EF and GH are parallel to each other. Show that ∠EOG ≅ ∠FOH
In the figure, ΔABC is an equilateral triangle. The angle bisector of ∠B will intersect the circumcircle ΔABC at point P. Then prove that: CQ = CA.

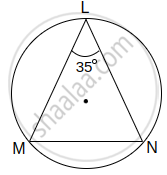
In the above figure, ∠L = 35°, find :
- m(arc MN)
- m(arc MLN)
Solution :
- ∠L = `1/2` m(arc MN) ............(By inscribed angle theorem)
∴ `square = 1/2` m(arc MN)
∴ 2 × 35 = m(arc MN)
∴ m(arc MN) = `square` - m(arc MLN) = `square` – m(arc MN) ...........[Definition of measure of arc]
= 360° – 70°
∴ m(arc MLN) = `square`
