Advertisements
Advertisements
प्रश्न
In the parking lot shown, the lines that mark the width space are parallel. If ∠1 =(x + 39)°, ∠2 = (2x – 3y)° find x and y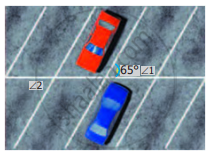
उत्तर
From the picture
∠2 + 65° = 180° ...[Sum of interior angles on the same side of a transversal]
x + 39° + 65° = 180°
x + 104° = 180°
x + 104° – 104° = 180° – 104°
x = 76°
Also from the picture
∠1 = 65° ...[alternate exterior angles]
2x – 3y = 65°
2(76) – 3y = 65°
152° – 3y = 65°
152° – 3y – 152° = 65 – 152°
– 3y = – 87
y = `(-87)/(-3)`
y = 29°
x = 76°, y = 29°
APPEARS IN
संबंधित प्रश्न
Find the measure of angle y in the following figure
Find the measure of angle z in the following figure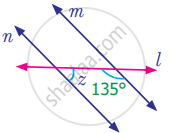
Find the measure of angle z in the following figure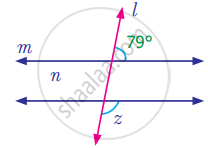
Find the value of angle a in the following figure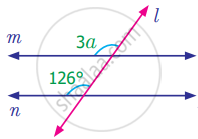
Two parallel lines are intersected by a transversal. What is the minimum number of angles you need to know to find the remaining angles. Give reason
A plumber must install pipe 2 parallel to pipe 1. He knows that ∠1 is 53. What is the measure of ∠2?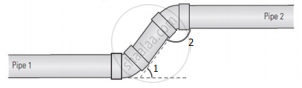
Find the value of z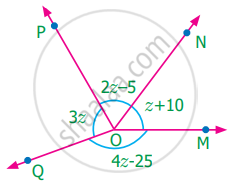
In the figure, the lines GH and IJ are parallel. If ∠1 = 108° and ∠2 = 123°, find the value of x, y and z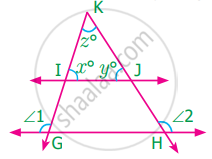
If a transversal intersects two parallel lines, then sum of interior angles on the same side of a transversal is ______.
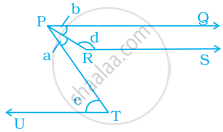
In the given figure, PQ, RS and UT are parallel lines. If c = 57° and a = `c/3`, find the value of d.