Advertisements
Advertisements
Question
In the parking lot shown, the lines that mark the width space are parallel. If ∠1 =(x + 39)°, ∠2 = (2x – 3y)° find x and y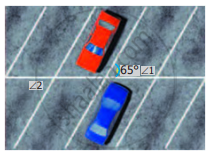
Solution
From the picture
∠2 + 65° = 180° ...[Sum of interior angles on the same side of a transversal]
x + 39° + 65° = 180°
x + 104° = 180°
x + 104° – 104° = 180° – 104°
x = 76°
Also from the picture
∠1 = 65° ...[alternate exterior angles]
2x – 3y = 65°
2(76) – 3y = 65°
152° – 3y = 65°
152° – 3y – 152° = 65 – 152°
– 3y = – 87
y = `(-87)/(-3)`
y = 29°
x = 76°, y = 29°
APPEARS IN
RELATED QUESTIONS
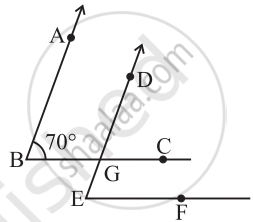
In the given figure, the arms of two angles are parallel.
If ∠ABC = 70°, then find
- ∠DGC
- ∠DEF
Find the measure of angle x in the following figure
Find the measure of angle z in the following figure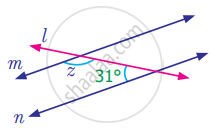
Find the measure of angle z in the following figure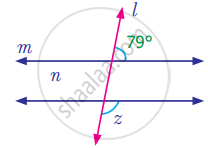
Find the value of angle a in the following figure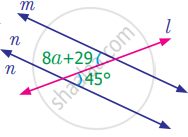
Anbu has marked the angles as shown in the following figure. Check whether it is correct. Give reason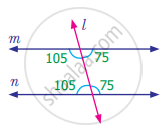
In the figure AB is parallel to DC. Find the value of ∠1 and ∠2. Justify your answer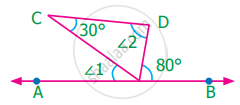
Find the value of z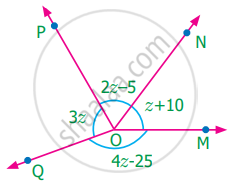
In the figure, the lines GH and IJ are parallel. If ∠1 = 108° and ∠2 = 123°, find the value of x, y and z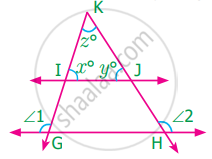
Anbu has marked the angles as shown in the following figure. Check whether it is correct. Give reason