Advertisements
Advertisements
Question
Draw two parallel lines and a transversal. Mark two corresponding angles A and B. If ∠A = 4x, and ∠B = 3x + 7, find the value of x. Explain
Solution
Let m and n are two parallel lines and l is the transversal.
A and B are corresponding angles.
We know that corresponding angles are equals,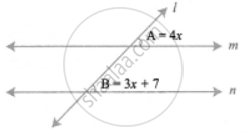
∴ 4x = 3x + 7
4x − 3x = 3x + 7 − 3x
x = 7°
∴ ∠A = 4 × 7 = 28° and ∠B = 3(7) + 7
= 21 + 7
= 28°
APPEARS IN
RELATED QUESTIONS
In the figure, AB is parallel to CD, find x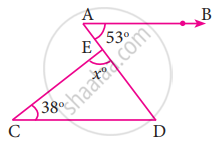
The sum of all angles at a point is
Find the measure of angle x in the following figure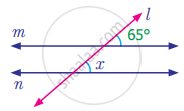
Find the measure of angle z in the following figure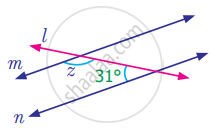
Find the value of angle a in the following figure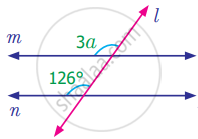
In the figure AB is parallel to DC. Find the value of ∠1 and ∠2. Justify your answer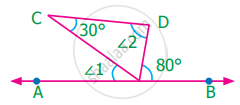
In the figure, the lines GH and IJ are parallel. If ∠1 = 108° and ∠2 = 123°, find the value of x, y and z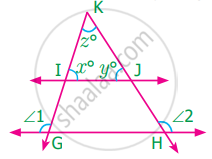
Two parallel lines are cut by transversal. If one angle of a pair of corresponding angles can be represented by 42° less than three times the other. Find the corresponding angles
If a transversal intersects two parallel lines, then corresponding angles are on the ______ side of the transversal.
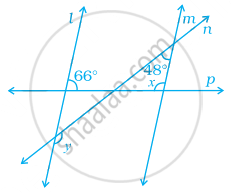
In the given figure, two parallel lines l and m are cut by two transversals n and p. Find the values of x and y.