Advertisements
Advertisements
Question
Two parallel lines are cut by transversal. If one angle of a pair of corresponding angles can be represented by 42° less than three times the other. Find the corresponding angles
Solution
We know that the corresponding angles are equal.
Let one of the corresponding angles be x.
Then the other will be 3x – 42°.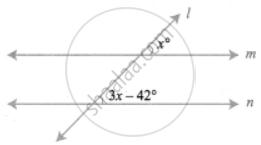
∴ 3x − 42° = x°
3x − 42° + 42° = x° + 42°
3x° = x + 42°
3x° − x° = x + 42° − x
2x = 42°
x = `42/2`
x = 21°
∴ The corresponding angles are 21° each
APPEARS IN
RELATED QUESTIONS
Find the measure of angle x in the following figure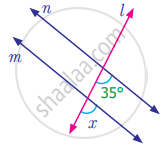
Find the measure of angle x in the following figure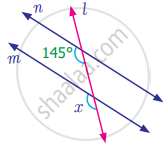
Find the measure of angle x in the following figure
Find the measure of angle y in the following figure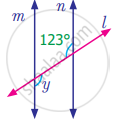
Find the value of angle a in the following figure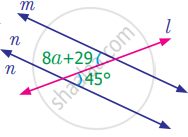
In the figure AB is parallel to DC. Find the value of ∠1 and ∠2. Justify your answer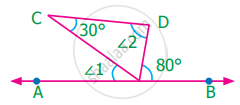
In the parking lot shown, the lines that mark the width space are parallel. If ∠1 =(x + 39)°, ∠2 = (2x – 3y)° find x and y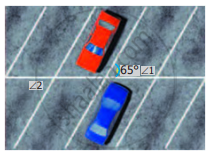
Draw two parallel lines and a transversal. Mark two corresponding angles A and B. If ∠A = 4x, and ∠B = 3x + 7, find the value of x. Explain
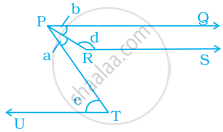
In the given figure, PQ, RS and UT are parallel lines. If c = 75° and a = `2/5`c, find b.
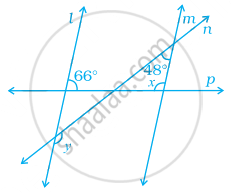
In the given figure, two parallel lines l and m are cut by two transversals n and p. Find the values of x and y.