Advertisements
Advertisements
प्रश्न
Is work-energy theorem valid in non-inertial frames?
उत्तर
In an non-inertial frame, pseudo force also comes into account. As we know that pseudo force does not exist, work-energy theorem is not valid in non-inertial frames.
APPEARS IN
संबंधित प्रश्न
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. what are the initial and final kinetic energies of the ball?
A ball is given a speed v on a rough horizontal surface. The ball travels through a distance l on the surface and stops. What is the work done by the kinetic friction?
Consider the situation of the previous question from a frame moving with a speed v0 parallel to the initial velocity of the block. (a) What are the initial and final kinetic energies? (b) What is the work done by the kinetic friction?
The US athlete Florence Griffith-Joyner won the 100 m sprint gold medal at Seoul Olympics in 1988, setting a new Olympic record of 10⋅54 s. Assume that she achieved her maximum speed in a very short time and then ran the race with that speed till she crossed the line. Take her mass to be 50 kg. What power Griffith-Joyner had to exert to maintain uniform speed?
In a factory, 2000 kg of metal needs to be lifted by an engine through a distance of 12 m in 1 minute. Find the minimum horsepower of the engine to be used.
A block of mass 30 kg is being brought down by a chain. If the block acquires a speed of 40 cm/s in dropping down 2 m, find the work done by the chain during the process.
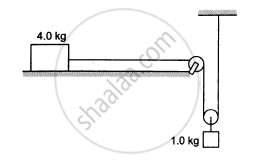
Consider the situation shown in the following figure. The system is released from rest and the block of mass 1 kg is found to have a speed 0⋅3 m/s after it has descended a distance of 1 m. Find the coefficient of kinetic friction between the block and the table.
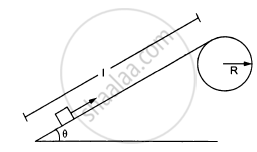
A small block of mass 200 g is kept at the top of a frictionless incline which is 10 m long and 3⋅2 m high. How much work was required (a) to lift the block from the ground and put it an the top, (b) to slide the block up the incline? What will be the speed of the block when it reaches the ground if (c) it falls off the incline and drops vertically to the ground (d) it slides down the incline? Take g = 10 m/s2.
A simple pendulum of length L with a bob of mass m is deflected from its rest position by an angle θ and released (following figure). The string hits a peg which is fixed at a distance x below the point of suspension and the bob starts going in a circle centred at the peg. (a) Assuming that initially the bob has a height less than the peg, show that the maximum height reached by the bob equals its initial height. (b) If the pendulum is released with \[\theta = 90^\circ \text{ and x = L}/2\] , find the maximum height reached by the bob above its lowest position before the string becomes slack. (c) Find the minimum value of x/L for which the bob goes in a complete circle about the peg when the pendulum is released from \[\theta = 90^\circ \]

Figure ( following ) shows a smooth track which consists of a straight inclined part of length l joining smoothly with the circular part. A particle of mass m is projected up the incline from its bottom. Find the minimum projection-speed \[\nu_0\] for which the particle reaches the top of the track.
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Find the gravitational potential energy of the chain with reference level at the centre of the sphere.
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Suppose the chain is released and slides down the sphere. Find the kinetic energy of the chain, when it has slid through an angle θ.
A chain of length l and mass m lies on the surface of a smooth sphere of radius R > l with one end tied to the top of the sphere. Find the tangential acceleration \[\frac{d\nu}{dt}\] of the chain when the chain starts sliding down.
A smooth sphere of radius R is made to translate in a straight line with a constant acceleration a. A particle kept on the top of the sphere is released at zero velocity with respect to the sphere. Find the speed of the particle with respect to the sphere as a function of the angle θ it slides.
A man, of mass m, standing at the bottom of the staircase, of height L climbs it and stands at its top.
- Work done by all forces on man is equal to the rise in potential energy mgL.
- Work done by all forces on man is zero.
- Work done by the gravitational force on man is mgL.
- The reaction force from a step does not do work because the point of application of the force does not move while the force exists.
A raindrop of mass 1.00 g falling from a height of 1 km hits the ground with a speed of 50 ms–1. Calculate
- the loss of P.E. of the drop.
- the gain in K.E. of the drop.
- Is the gain in K.E. equal to a loss of P.E.? If not why.
Take g = 10 ms–2
Suppose the average mass of raindrops is 3.0 × 10–5 kg and their average terminal velocity 9 ms–1. Calculate the energy transferred by rain to each square metre of the surface at a place which receives 100 cm of rain in a year.
