Advertisements
Advertisements
प्रश्न
किसी 200 m ऊँची खड़ी चट्टान के किनारे से दो पत्थरों को एक साथ ऊपर की ओर 15 m s-1 तथा 30 m s-1 की प्रारंभिक चाल से फेंका जाता है। इसका सत्यापन कीजिए कि संलग्न ग्राफ पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है। वायु के प्रतिरोध को नगण्य मानिए और यह मानिए कि जमीन से टकराने के बाद पत्थर ऊपर की ओर उछलते नहीं। मान लीजिए g = 10 m s-2 । ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए।
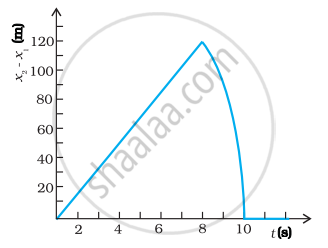
उत्तर
पहले पत्थर के लिए,
x(0) = 200 m, ν(0) = 15 m s-1, a = -10 m s-2
अतः t समय पर पहले पत्थर की स्थिति
`"x"_1("t") = "x"(0) + "ν"(0)"t" + 1/2 "a" "t"^2 = 200 + 15 "t" - 5 "t"^2` ...(1)
जब पहला पत्थर जमीं से टकराता है,
`"x"_1("t") = 0 ` या `-5 "t"^2 + 15 "t" + 200 = 0` ...(2)
इसी प्रकार दूसरे पत्थर के लिए,
x(0) = 200 m, ν(0) = 30 m s-1, a = 10 m s-2
अतः t समय पर दूसरे पत्थर की स्थिति
`"x"_2("t") = "x"(0) + "ν"(0) "t" + 1/2 "a" "t"^2 = 200 + 30 "t" - 5 "t"^2` .....(3)
दूसरे पत्थर की पहले पत्थर के सापेक्ष आपेक्षिक स्थिति समिकरण (1) को समीकरण (3) में से घटाकर निम्नवत दी जा सकती है-
x2 (t) - x1(t) = 15 t ...(4)
या x= 15 t ....(5)
जहाँ, x = x2(t) - x1(t), दोनों पत्थरों के बीच पृथक्करण है।
स्पष्ट है की x ∝ t अर्थात जब तक दोनों पत्थर गति करते रहेंगे, उनके बीच पृथक्करण बढ़ता जायेगा।
चूँकि x2(t) - x1(t) तथा t के बीच एक रेखीय संबंध है, इसलिए ग्राफ एक सीधी रेखा होगा। समीकरण (2) को हल करने पर t = 8s अर्थात 8 s बाद पहला पत्थर पृथ्वी पर गिर जायेगा। इसके बाद केवल एक ही पत्थर गति की अवस्था में होगा, अतः इस क्षण (t = 8s पर) दोनों के बीच पृथक्करण अधिकतम होगा। अतः समीकरण (4) में t = 8s रखने पर अधिकतम पृथक्करण 120 m है।
8 s बाद, केवल दूसरा पत्थर गति की अवस्था में होगा; अतः ग्राफ द्विघाती समीकरण के अनुसार परवलयाकार होगा।
APPEARS IN
संबंधित प्रश्न
सीधे राजमार्ग पर कोई कार 126 kmh-1 की चाल से चल रही है। इसे 200 m की दूरी पर रोक दिया जाता है। कार के मंदन को एकसमान मानिए और इसका मान निकालिए। कार को रुकने में कितना समय लगा?
दो रेलगाड़ियाँ A व B दो समांतर पटरियों पर 72 kmh-1 की एकसमान चाल से एक ही दिशा में चल रही हैं। प्रत्येक गाड़ी 400 m लंबी है और गाड़ी A गाड़ी B से आगे है। B का चालक A से आगे निकलना चाहता है तथा 1 ms-2 से इसे त्वरित करता है। यदि 50 s के बाद B को गार्ड A के चालक से आगे हो जाता है तो दोनों के बीच आरंभिक दूरी कितनी थी?
कोई खिलाड़ी एक गेंद को ऊपर की ओर आरंभिक चाल 29 ms-1 से फेंकता है,
- गेंद की ऊपर की ओर गति के दौरान त्वरण की दिशा क्या होगी?
- इसकी गति के उच्चतम बिंदु पर गेंद के वेग व त्वरण क्या होंगे?
- गेंद के उच्चतम बिंदु पर स्थान के समय को x= 0 व t = 0 चुनिए, ऊध्र्वाधर नीचे की ओर की दिशा को x-अक्ष की धनात्मक दिशा मानिए। गेंद की ऊपर की व नीचे की ओर गति के दौरान स्थिति, वेग व त्वरण के चिह्न बताइए।
- किस ऊँचाई तक गेंद ऊपर जाती है और कितनी देर के बाद गेंद खिलाड़ी के हाथों में आ जाती है? [g = 9.8m s-2 तथा वायु का प्रतिरोध नगण्य है।]
किसी गेंद को 90 m की ऊँचाई से फर्श पर गिराया जाता है। फर्श के साथ प्रत्येक टक्कर में गेंद की चाल `1/10` कम हो जाती है। इसकी गति का t= 0 से 12 s के बीच चाल-समय ग्राफ खींचिए।
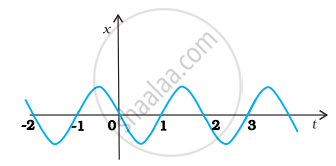
नीचे दिए गए चित्र में किसी कण की एकविमीय सरल आवर्ती गति के लिए x - t ग्राफ दिखाया गया है। समय t = 0.3 s, 1.2 s, – 1.2s पर कण के स्थिति, वेग व त्वरण के चिह्न क्या होंगे?
कोई तीन पहिये वाला स्कूटर अपनी विरामावस्था से गति प्रारंभ करता है। फिर 10 s तक किसी सीधी सड़क पर 1m s-2 के एकसमान त्वरण से चलता है। इसके बाद वह एकसमान वेग से चलता है। स्कूटर द्वारा n वें सेकंड (n= 1, 2, 3, ……) में तय की गई दूरी को n के सापेक्ष आलेखित कीजिए। आप क्या आशा करते हैं कि त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा?
किसी स्थिर लिफ्ट में (जो ऊपर से खुली है) कोई बालक खड़ा है। वह अपने पूरे जोर से एक गेंद ऊपर की ओर फेंकता है जिसकी प्रारंभिक चाल 49 ms-1 है। उसके हाथों में गेंद के वापस आने में कितना समय लगेगा? यदि लिफ्ट ऊपर की ओर 5 m s-1 की एकसमान चाल से गति करना प्रारंभ कर दे और वह बालक फिर गेंद को अपने पूरे जोर से फेंकता तो कितनी देर में गेंद उसके हाथों में लौट आएगी?
