Question

 किसी गोले का, इसके किसी व्यास के परितः जड़त्व - आघूर्ण 2MR²/5 है, जहाँ M गोले का द्रव्यमान एवं R इसकी त्रिज्या है। गोले पर खींची गई स्पर्श रेखा के परितः इसका जड़त्व - आघूर्ण ज्ञात कीजिए।

Answer 1

दिया है : गोले का द्रव्यमान = M, त्रिज्या = R

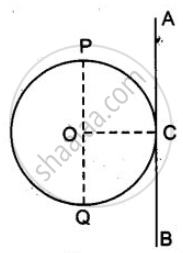
रेखा AB गोले की एक स्पर्श रेखा है जिसके परितः गोले का जड़त्व-आघूर्ण ज्ञात करना है। स्पर्श रेखा AB के समान्तर, गोले का एक व्यास PQ खींचा।

प्रश्नानुसार, व्यास PQ (जो कि गोले के केन्द्र से जाता है) के परितः गोले का जड़त्व-आघूर्ण।

`"I"_"G" = 2/5 "MR"^2`

समान्तर अक्षों की प्रमेय से,

स्पर्श रेखा AB के परितः गोले का जड़त्व - आघूर्ण

`"I" = "I"_"G" + "Md"^2`

(d = समान्तर अक्षों के बीच की दूरी = OC = R)

= `2/5  "MR"^2 + "MR"^2`

`"I" = 7/5  "MR"^2`