Advertisements
Advertisements
प्रश्न
Laser light of wavelength 630 nm is incident on a pair of slits which are separated by 1.8 mm. If the screen is kept 80 cm away from the two slits, calculate:
1) fringe separation i.e. fringe width.
2) distance of 10th bright fringe from the centre of the interference pattern
उत्तर
`lambda = 630 nm`
`d = 1.8 xx 10^(-3)`
D = 0.80 m
1) `beta = (lambdaD)/d = (630 xx 10^(-9)xx 0.8)/(1.8 xx 10^(-3) ) = 2.8 xx 10^(-4) m`
2) `x = (nlambdaD)/d = 10 xx 2.8 xx 10^(-4) = 2.8 xx 10^(-3) m`
APPEARS IN
संबंधित प्रश्न
The intensity at the central maximum (O) in a Young’s double slit experimental set-up shown in the figure is IO. If the distance OP equals one-third of the fringe width of the pattern, show that the intensity at point P, would equal `(I_0)/4`.

Why two light sources must be of equal intensity to obtain a well-defined interference pattern?
What are coherent sources of light?
What is phase of a wave?
What is intensity (or) amplitude division?
What is a bandwidth of interference pattern?
A graph is plotted between the fringe-width Z and the distance D between the slit and eye-piece, keeping other adjustment same. The correct graph is
A.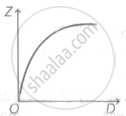 |
B. |
C.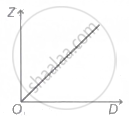 |
D.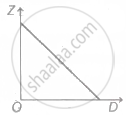 |
A wire of length 'L' and area of cross-section · A' is made of material of Young's modulus 'Y'. It is stretched by an amount 'x'. The work done in stretching the wire is ______.
If two waves represented by `"y"_1 = 3 "sin" omega "t"` and `"y"_2 = 5 "sin" (omega "t" + pi/3)` interfere at a point, then the amplitude of the resulting wave will be about ____________.
The interference pattern is obtained with two coherent light sources of intensity ratio 4 : 1. And the ratio `("I"_"max" - "I"_"min")/("I"_"max" + "I"_"min")` is `5/x`. Then the value of x will be equal to ______.
