Question

Let O(0, 0) and A(0, 1) be two fixed points. Then the locus of a point P such that the perimeter of ΔAOP is 4, is ______.

विकल्प

• 9x² – 8y² + 8y = 16

• 8x² – 9y² + 9y = 18

• 9x² + 8y² – 8y = 16

• 8x² + 9y² – 9y = 18

Answer 1

Let O(0, 0) and A(0, 1) be two fixed points. Then the locus of a point P such that the perimeter of ΔAOP is 4, is `underlinebb(9x^2 + 8"y"^2 - 8"y" = 16)`.

Explanation:

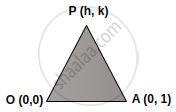
`1 + sqrt(("h" - 0)^2 + ("k" - 0)^2) + sqrt(("h" - 0)^2 + ("k" - 1)^2` = 4

`sqrt("h"^2 + ("k" - 1)^2) = 3 - sqrt("h"^2 + "k"^2)`

Squaring both the sides,

h² + k² – 2k + 1 = `9 + "h"^2 + "k"^2 - 6sqrt("h"^2 + "k"^2)`

⇒ –2k – 8 = `-6sqrt("h"^2 + "k"^2)`

⇒ k + 4 = `3sqrt("h"^2 + "k"^3)`

Squaring both the sides,

k² + 16 + 8k = 9h² + 9k²

9h² + 8k² – 8k – 16 = 0

Thus 9x² + 8y² – 8y – 16 = 0