Advertisements
Advertisements
प्रश्न
Maximize Z = 5x + 3y
Subject to
\[3x + 5y \leq 15\]
\[5x + 2y \leq 10\]
\[ x, y \geq 0\]
उत्तर
Region represented by 3x + 5y ≤ 15 :
The line 3x + 5y = 15 meets the coordinate axes at A(5,0) and B(0,3) respectively. By joining these points we obtain the line 3x + 5y = 15.
Clearly (0,0) satisfies the inequation 3x + 5y ≤ 15. So,the region containing the origin represents the solution set of the inequation 3x + 5y ≤ 15.
Region represented by 5x + 2y ≤ 10 :
The line 5x + 2y = 10 meets the coordinate axes at C(2,0) and D(0,5) respectively. By joining these points we obtain the line 5x + 2y = 10.
Clearly (0,0) satisfies the inequation 5x + 2y ≤ 10. So,the region containing the origin represents the solution set of the inequation 5x + 2y ≤ 10.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.The feasible region determined by the system of constraints, 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, and y ≥ 0, are as follows.
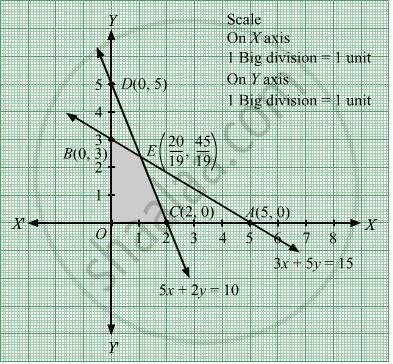
The values of Z at these corner points are as follows.
| Corner point | Z = 5x + 3y |
| O(0, 0) | 5 × 0 + 3 × 0 = 0 |
| C(2, 0) |
5 × 2 + 3 × 0 = 10
|
| \[E\left( \frac{20}{19}, \frac{45}{19} \right)\] |
5x \[\frac{20}{19}\] +3x \[\frac{45}{19}\] = \[\frac{235}{19}\] |
| B(0, 3) | 5 0 + 3 × 3 = 9 |
Therefore, the maximum value of Z is
Thus, the optimal value of Z is \[\frac{235}{19}\] .
APPEARS IN
संबंधित प्रश्न
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y
Subject to: x + 4y ≤ 24
3x + y ≤ 21
x + y ≤ 9
x ≥ 0, y ≥ 0
Maximise Z = x + 2y subject to the constraints
`x + 2y >= 100`
`2x - y <= 0`
`2x + y <= 200`
Solve the above LPP graphically
Solve the following LPP graphically :
Maximise Z = 105x + 90y
subject to the constraints
x + y ≤ 50
2x + y ≤ 80
x ≥ 0, y ≥ 0.
Minimize Z = 5x + 3y
Subject to
\[2x + y \geq 10\]
\[x + 3y \geq 15\]
\[ x \leq 10\]
\[ y \leq 8\]
\[ x, y \geq 0\]
Minimize Z = 30x + 20y
Subject to
\[x + y \leq 8\]
\[ x + 4y \geq 12\]
\[5x + 8y = 20\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
Subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = 3x1 + 4x2, if possible,
Subject to the constraints
\[x_1 - x_2 \leq - 1\]
\[ - x_1 + x_2 \leq 0\]
\[ x_1 , x_2 \geq 0\]
A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 of calories. Two foods A and B, are available at a cost of Rs 4 and Rs 3 per unit respectively. If one unit of A contains 200 units of vitamin, 1 unit of mineral and 40 calories and one unit of food B contains 100 units of vitamin, 2 units of minerals and 40 calories, find what combination of foods should be used to have the least cost?
One kind of cake requires 300 gm of flour and 15 gm of fat, another kind of cake requires 150 gm of flour and 30 gm of fat. Find the maximum number of cakes which can be made from 7.5 kg of flour and 600 gm of fat, assuming that there is no shortage of the other ingradients used in making the cake. Make it as an LPP and solve it graphically.
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no storage of the other ingredients used in making the cakes.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 2 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A firm manufactures two products A and B. Each product is processed on two machines M1 and M2. Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2. The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs 3 and Rs 4 respectively.
Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
A firm manufactures headache pills in two sizes A and B. Size A contains 2 grains of aspirin, 5 grains of bicarbonate and 1 grain of codeine; size B contains 1 grain of aspirin, 8 grains of bicarbonate and 66 grains of codeine. It has been found by users that it requires at least 12 grains of aspirin, 7.4 grains of bicarbonate and 24 grains of codeine for providing immediate effects. Determine graphically the least number of pills a patient should have to get immediate relief. Determine also the quantity of codeine consumed by patient.
A chemical company produces two compounds, A and B. The following table gives the units of ingredients, C and D per kg of compounds A and B as well as minimum requirements of C and D and costs per kg of A and B. Find the quantities of A and B which would give a supply of C and D at a minimum cost.
| Compound | Minimum requirement | ||
| A | B | ||
| Ingredient C Ingredient D |
1 3 |
2 1 |
80 75 |
| Cost (in Rs) per kg | 4 | 6 | - |
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats of first class. However, at least 4 times as many passengers prefer to travel by economy class to the first class. Determine how many each type of tickets must be sold in order to maximize the profit for the airline. What is the maximum profit.
A small firm manufacturers items A and B. The total number of items A and B that it can manufacture in a day is at the most 24. Item A takes one hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160, how many of each type of item be produced to maximize the profit? Solve the problem graphically.
A company manufactures two articles A and B. There are two departments through which these articles are processed: (i) assembly and (ii) finishing departments. The maximum capacity of the first department is 60 hours a week and that of other department is 48 hours per week. The product of each unit of article A requires 4 hours in assembly and 2 hours in finishing and that of each unit of B requires 2 hours in assembly and 4 hours in finishing. If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B, find the number of units of A and B to be produced per week in order to have maximum profit.
A manufacturer makes two products, A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 units of product A and 16 units of product B. A working week consists of 40 hours of production and the weekly turn over must not be less than Rs 10000. If the profit on each of product A is Rs 20 and an product B is Rs 30, then how many of each should be produced so that the profit is maximum? Also find the maximum profit.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time.
(i) What number of rackets and bats must be made if the factory is to work at full capacity?
(ii) If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity.
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at ₹7 profit and that of B at a profit of ₹4. Find the production level per day for maximum profit graphically.
The value of objective function is maximum under linear constraints ______.
Find the graphical solution for the system of linear inequation 2x + y ≤ 2, x − y ≤ 1
Draw the graph of inequalities x ≤ 6, y −2 ≤ 0, x ≥ 0, y ≥ 0 and indicate the feasible region
Area of the region bounded by y = cos x, x = 0, x = π and X-axis is ______ sq.units.
The feasible region of an LPP is shown in the figure. If z = 3x + 9y, then the minimum value of z occurs at ______.
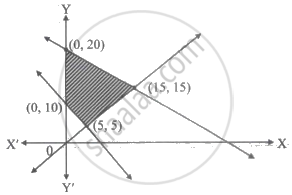
The maximum value of z = 3x + 10y subjected to the conditions 5x + 2y ≤ 10, 3x + 5y ≤ 15, x, y ≥ 0 is ______.
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of an L.P.P. is called its ____________.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then ____________.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
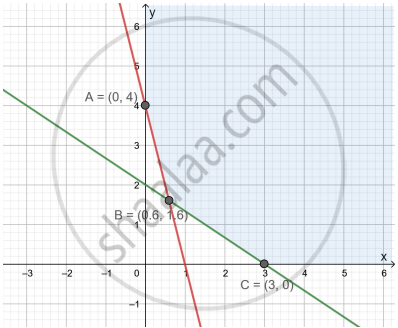
The corner points of the shaded unbounded feasible region of an LPP are (0, 4), (0.6, 1.6) and (3, 0) as shown in the figure. The minimum value of the objective function Z = 4x + 6y occurs at ______.
The maximum value of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
The maximum value of 2x + y subject to 3x + 5y ≤ 26 and 5x + 3y ≤ 30, x ≥ 0, y ≥ 0 is ______.
