Advertisements
Advertisements
प्रश्न
Minimize Z = 30x + 20y
Subject to
\[x + y \leq 8\]
\[ x + 4y \geq 12\]
\[5x + 8y = 20\]
\[ x, y \geq 0\]
उत्तर
First, we will convert the given inequations into equations, we obtain the following equations:
x + y = 8, x + 4y = 12, x = 0 and y = 0
5x + 8y = 20 is already an equation.
Region represented by x + y ≤ 8:
The line x + y = 8 meets the coordinate axes at A(8, 0) and B(0, 8) respectively. By joining these points we obtain the line x + y = 8.Clearly (0,0) satisfies the inequation x+ y ≤ 8. So,the region in xy plane which contain the origin represents the solution set of the inequation x + y ≤ 8.
Region represented by x + 4y ≥ 12:
The line x + 4y = 12 meets the coordinate axes at C(12, 0) and D(0, 3) respectively. By joining these points we obtain the line x + 4y = 12.Clearly (0,0) satisfies the inequation x + 4y ≥ 12. So,the region in xy plane which does not contain the origin represents the solution set of the inequation x + 4y ≥ 12.
The line 5x + 8y = 20 is the line that passes through E(4, 0) and \[F\left( 0, \frac{5}{2} \right)\] Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints, x + y ≤ 8, x + 4y ≥ 12, 5x+ 8y = 20, x ≥ 0 and y ≥ 0 are as follows.
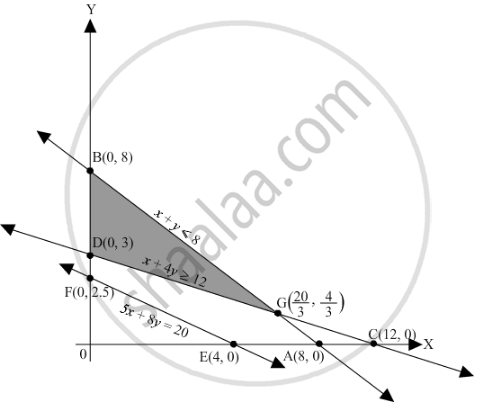
The corner points of the feasible region are B(0,8), D(0,3),
The values of Z at these corner points are as follows.
| Corner point | Z = 30x + 20y |
| B(0,8) | 160 |
| D(0,3) | 60 |
|
\[G\left( \frac{20}{3}, \frac{4}{3} \right)\]
|
266.66 |
Therefore, the minimum value of Z is 60 at the point D(0,3). Hence, x = 0 and y =3 is the optimal solution of the given LPP.
Thus, the optimal value of Z is 60
APPEARS IN
संबंधित प्रश्न
There are two types of fertilisers 'A' and 'B'. 'A' consists of 12% nitrogen and 5% phosphoric acid whereas 'B' consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If 'A' costs Rs 10 per kg and 'B' cost Rs 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost
Minimum and maximum z = 5x + 2y subject to the following constraints:
x-2y ≤ 2
3x+2y ≤ 12
-3x+2y ≤ 3
x ≥ 0,y ≥ 0
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs 7 profit and B at a profit of Rs 4. Find the production level per day for maximum profit graphically.
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Solve the following linear programming problem graphically :
Maximise Z = 7x + 10y subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Maximize Z = 9x + 3y
Subject to
\[2x + 3y \leq 13\]
\[ 3x + y \leq 5\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
Subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = 3x + 3y, if possible,
Subject to the constraints
\[x - y \leq 1\]
\[x + y \geq 3\]
\[ x, y \geq 0\]
Show the solution zone of the following inequalities on a graph paper:
\[5x + y \geq 10\]
\[ x + y \geq 6\]
\[x + 4y \geq 12\]
\[x \geq 0, y \geq 0\]
Find x and y for which 3x + 2y is minimum subject to these inequalities. Use a graphical method.
A diet of two foods F1 and F2 contains nutrients thiamine, phosphorous and iron. The amount of each nutrient in each of the food (in milligrams per 25 gms) is given in the following table:
Nutrients |
Food |
F1 | F2 |
| Thiamine | 0.25 | 0.10 |
|
| Phosphorous | 0.75 | 1.50 | |
| Iron | 1.60 | 0.80 | |
The minimum requirement of the nutrients in the diet are 1.00 mg of thiamine, 7.50 mg of phosphorous and 10.00 mg of iron. The cost of F1 is 20 paise per 25 gms while the cost of F2 is 15 paise per 25 gms. Find the minimum cost of diet.
A hospital dietician wishes to find the cheapest combination of two foods, A and B, that contains at least 0.5 milligram of thiamin and at least 600 calories. Each unit of Acontains 0.12 milligram of thiamin and 100 calories, while each unit of B contains 0.10 milligram of thiamin and 150 calories. If each food costs 10 paise per unit, how many units of each should be combined at a minimum cost?
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no storage of the other ingredients used in making the cakes.
A manufacturer has three machines installed in his factory. machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day. He produces only two items, each requiring the use of three machines. The number of hours required for producing one unit each of the items on the three machines is given in the following table:
| Item | Number of hours required by the machine | ||
A B |
I | II | III |
| 1 2 |
2 1 |
1 5/4 |
|
He makes a profit of Rs 6.00 on item A and Rs 4.00 on item B. Assuming that he can sell all that he produces, how many of each item should he produces so as to maximize his profit? Determine his maximum profit. Formulate this LPP mathematically and then solve it.
A small manufacturer has employed 5 skilled men and 10 semi-skilled men and makes an article in two qualities deluxe model and an ordinary model. The making of a deluxe model requires 2 hrs. work by a skilled man and 2 hrs. work by a semi-skilled man. The ordinary model requires 1 hr by a skilled man and 3 hrs. by a semi-skilled man. By union rules no man may work more than 8 hrs per day. The manufacturers clear profit on deluxe model is Rs 15 and on an ordinary model is Rs 10. How many of each type should be made in order to maximize his total daily profit.
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?
A chemical company produces two compounds, A and B. The following table gives the units of ingredients, C and D per kg of compounds A and B as well as minimum requirements of C and D and costs per kg of A and B. Find the quantities of A and B which would give a supply of C and D at a minimum cost.
| Compound | Minimum requirement | ||
| A | B | ||
| Ingredient C Ingredient D |
1 3 |
2 1 |
80 75 |
| Cost (in Rs) per kg | 4 | 6 | - |
A company manufactures two types of novelty Souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours available for assembling. The profit is 50 paise each for type A and 60 paise each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats of first class. However, at least 4 times as many passengers prefer to travel by economy class to the first class. Determine how many each type of tickets must be sold in order to maximize the profit for the airline. What is the maximum profit.
A gardener has supply of fertilizer of type I which consists of 10% nitrogen and 6% phosphoric acid and type II fertilizer which consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, he finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for his crop. If the type I fertilizer costs 60 paise per kg and type II fertilizer costs 40 paise per kg, determine how many kilograms of each fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
Anil wants to invest at most Rs 12000 in Saving Certificates and National Saving Bonds. According to rules, he has to invest at least Rs 2000 in Saving Certificates and at least Rs 4000 in National Saving Bonds. If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bond is 10% per annum, how much money should he invest to earn maximum yearly income? Find also his maximum yearly income.
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A manufacturer makes two products, A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 units of product A and 16 units of product B. A working week consists of 40 hours of production and the weekly turn over must not be less than Rs 10000. If the profit on each of product A is Rs 20 and an product B is Rs 30, then how many of each should be produced so that the profit is maximum? Also find the maximum profit.
A small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is at most 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs 300 and that on a chain is Rs 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an LPP and solve it graphically.
From the details given below, calculate the five-year moving averages of the number of students who have studied in a school. Also, plot these and original data on the same graph paper.
| Year | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| Number of Students | 332 | 317 | 357 | 392 | 402 | 405 | 410 | 427 | 405 | 438 |
A company manufactures two types of cardigans: type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the company. Solve it graphically and find the maximum profit.
For L.P.P. maximize z = 4x1 + 2x2 subject to 3x1 + 2x2 ≥ 9, x1 - x2 ≤ 3, x1 ≥ 0, x2 ≥ 0 has ______.
Area of the region bounded by y = cos x, x = 0, x = π and X-axis is ______ sq.units.
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
If 4x + 5y ≤ 20, x + y ≥ 3, x ≥ 0, y ≥ 0, maximum 2x + 3y is ______.
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
A feasible solution to a linear programming problem
The constraints –x1 + x2 ≤ 1, –x1 + 3x2 ≤ 9, x1x2 ≥ 0 define on ______.
The objective function Z = x1 + x2, subject to the constraints are x1 + x2 ≤ 10, – 2x1 + 3x2 ≤ 15, x1 ≤ 6, x1, x2 ≥ 0, has maximum value ______ of the feasible region.
Solve the following Linear Programming problem graphically:
Maximize: Z = 3x + 3.5y
Subject to constraints:
x + 2y ≥ 240,
3x + 1.5y ≥ 270,
1.5x + 2y ≤ 310,
x ≥ 0, y ≥ 0.
