Advertisements
Advertisements
प्रश्न
Solve the following linear programming problem graphically :
Maximise Z = 7x + 10y subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
उत्तर
The given constraints are 4x + 6y ≤ 240, 6x + 3y ≤ 240, x ≥ 10, x ≥ 0, y ≥ 0.
Firstly, convert the given inequations into equations, we obtain the following equations:
4x + 6y = 240, 6x + 3y = 240, x = 10, x = 0 and y = 0.
The line 4x + 6y = 240 meets the coordinate axes at A1(60, 0) and B1(0, 40), respectively. Join these points to obtain the line 4x + 6y = 240
Clearly (0,0) satisfies the inequation 4x + 6y ≤ 240. So, the region containing the origin represents the solution set of the inequation 4x + 6y ≤ 240.
The line 6x + 3y = 240 meets the coordinate axes at A2(40, 0) and B2(0, 80), respectively. Join these points to obtain the line 6x + 3y = 240.
Clearly (0,0) satisfies the inequation 6x + 3y ≤ 240. So, the region containing the origin represents the solution set of the inequation 6x + 3y ≤ 240.
The line x = 10 is the line that passes through A3(10, 0) and parallel to y-axis.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints is shown below:
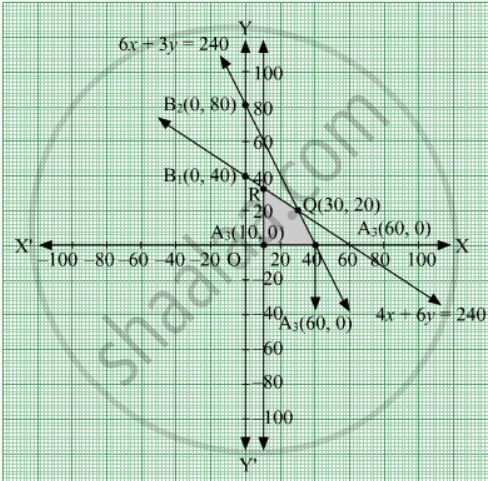
The corner points of the feasible region are A3(10, 0), A2(40, 0), Q(30, 20) and R (20, `80/3`)
The values of Z at these corner points are as follows:
| Corner point | Value of the objective function Z = 7x + 10y |
| A3(10, 0) | Z = 7 × 10 + 10 × 0 = 70 |
| A2(40, 0) | Z = 7 × 40 + 10 × 0 = 280 |
| Q(30, 20) | Z = 7 × 30 + 10 × 20 = 410 (Maximum) |
| R(20, 80/3) | `Z = 7 xx 20 + xx 80/3 = 1220/3` |
Thus, the maximum value of the objective function Z is 410 which is obtained at x = 30 and y = 20.
APPEARS IN
संबंधित प्रश्न
Solve the following LPP by using graphical method.
Maximize : Z = 6x + 4y
Subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Also find maximum value of Z.
Minimize :Z=6x+4y
Subject to : 3x+2y ≥12
x+y ≥5
0 ≤x ≤4
0 ≤ y ≤ 4
Minimum and maximum z = 5x + 2y subject to the following constraints:
x-2y ≤ 2
3x+2y ≤ 12
-3x+2y ≤ 3
x ≥ 0,y ≥ 0
Maximize Z = 4x + 3y
subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = −x1 + 2x2
Subject to
\[- x_1 + 3 x_2 \leq 10\]
\[ x_1 + x_2 \leq 6\]
\[ x_1 - x_2 \leq 2\]
\[ x_1 , x_2 \geq 0\]
Solved the following linear programming problem graphically:
Maximize Z = 60x + 15y
Subject to constraints
\[x + y \leq 50\]
\[3x + y \leq 90\]
\[ x, y \geq 0\]
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below:
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 2 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A fruit grower can use two types of fertilizer in his garden, brand P and Q. The amounts (in kg) of nirogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicates that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
| kg per bag | ||
| Brand P | Brand P | |
| Nitrogen | 3 | 3.5 |
| Phosphoric acid | 1 | 2 |
| Potash | 3 | 1.5 |
| Chlorine | 1.5 | 2 |
If the grower wants to minimize the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?
A factory manufactures two types of screws, A and B, each type requiring the use of two machines - an automatic and a hand-operated. It takes 4 minute on the automatic and 6 minutes on the hand-operated machines to manufacture a package of screws 'A', while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machine to manufacture a package of screws 'B'. Each machine is available for at most 4 hours on any day. The manufacturer can sell a package of screws 'A' at a profit of 70 P and screws 'B' at a profit of Rs 1. Assuming that he can sell all the screws he can manufacture, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
A small manufacturer has employed 5 skilled men and 10 semi-skilled men and makes an article in two qualities deluxe model and an ordinary model. The making of a deluxe model requires 2 hrs. work by a skilled man and 2 hrs. work by a semi-skilled man. The ordinary model requires 1 hr by a skilled man and 3 hrs. by a semi-skilled man. By union rules no man may work more than 8 hrs per day. The manufacturers clear profit on deluxe model is Rs 15 and on an ordinary model is Rs 10. How many of each type should be made in order to maximize his total daily profit.
A manufacturer of patent medicines is preparing a production plan on medicines, A and B. There are sufficient raw materials available to make 20000 bottles of A and 40000 bottles of B, but there are only 45000 bottles into which either of the medicines can be put. Further, it takes 3 hours to prepare enough material to fill 1000 bottles of A, it takes 1 hour to prepare enough material to fill 1000 bottles of B and there are 66 hours available for this operation. The profit is Rs 8 per bottle for A and Rs 7 per bottle for B. How should the manufacturer schedule his production in order to maximize his profit?
Anil wants to invest at most Rs 12000 in Saving Certificates and National Saving Bonds. According to rules, he has to invest at least Rs 2000 in Saving Certificates and at least Rs 4000 in National Saving Bonds. If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bond is 10% per annum, how much money should he invest to earn maximum yearly income? Find also his maximum yearly income.
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp while it takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at most 20 hours and the grinding/cutting machine for at most 12 hours. The profit from the sale of a lamp is ₹5.00 and a shade is ₹3.00. Assuming that the manufacturer sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
A small firm manufacturers items A and B. The total number of items A and B that it can manufacture in a day is at the most 24. Item A takes one hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160, how many of each type of item be produced to maximize the profit? Solve the problem graphically.
A small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is at most 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs 300 and that on a chain is Rs 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an LPP and solve it graphically.
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weigh 1 kg and \[1\frac{1}{2}\] kg each respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the books of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically.
Find the feasible solution of linear inequation 2x + 3y ≤ 12, 2x + y ≤ 8, x ≥ 0, y ≥ 0 by graphically
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at ____________.
A feasible solution to a linear programming problem
The comer point of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let x = Px + qx where P, q > 0 condition on P and Q so that the maximum of z occurs at both (3, 4) and (0, 5) is
The objective function Z = x1 + x2, subject to the constraints are x1 + x2 ≤ 10, – 2x1 + 3x2 ≤ 15, x1 ≤ 6, x1, x2 ≥ 0, has maximum value ______ of the feasible region.
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
Minimize z = x + 2y,
Subject to x + 2y ≥ 50, 2x – y ≤ 0, 2x + y ≤ 100, x ≥ 0, y ≥ 0.
If x – y ≥ 8, x ≥ 3, y ≥ 3, x ≥ 0, y ≥ 0 then find the coordinates of the corner points of the feasible region.
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
