Advertisements
Advertisements
प्रश्न
A factory manufactures two types of screws, A and B, each type requiring the use of two machines - an automatic and a hand-operated. It takes 4 minute on the automatic and 6 minutes on the hand-operated machines to manufacture a package of screws 'A', while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machine to manufacture a package of screws 'B'. Each machine is available for at most 4 hours on any day. The manufacturer can sell a package of screws 'A' at a profit of 70 P and screws 'B' at a profit of Rs 1. Assuming that he can sell all the screws he can manufacture, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
उत्तर
Let the factory manufacture x screws of type A and y screws of type B on each day. Therefore,
x ≥ 0 and y ≥ 0
The given information can be compiled in a table as follows.
| Screw A | Screw B | Availability | |
| Automatic Machine (min) | 4 | 6 | 4 × 60 = 240 |
| Hand Operated Machine (min) | 6 | 3 | 4 × 60 = 240 |
\[4x + 6y \geq 240\]
The manufacturer can sell a package of screws 'A' at a profit of Rs 0.7 and screws 'B' at a profit of Re 1.
Total profit, Z = 0.7x + 1y
The mathematical formulation of the given problem is
Maximize Z = 0.7x + 1y
subject to the constraints,
x, y ≥ 0
First we will convert inequations into equations as follows:
4x + 6y = 240, 6x + 3y = 240, x = 0 and y = 0
Region represented by 4x + 6y ≤ 240:
The line 4x + 6y = 240 meets the coordinate axes at A1(60, 0) and B1(0, 40) respectively. By joining these points we obtain the line 4x + 6y = 240. Clearly (0,0) satisfies the 4x + 6y = 240. So,the region which contains the origin represents the solution set of the inequation 4x + 6y ≤ 240.
Region represented by 6x + 3y ≤ 240:
The line 6x + 3y = 240 meets the coordinate axes at C1(40, 0) and D1(0, 80) respectively. By joining these points we obtain the line 6x + 3y = 240. Clearly (0,0) satisfies the inequation 6x + 3y ≤ 240. So,the region which contains the origin represents the solution set of the inequation 6x + 3y ≤ 240.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 4x + 6y ≤ 240, 6x + 3y ≤ 240, x ≥ 0, and y ≥ 0 are as follows.
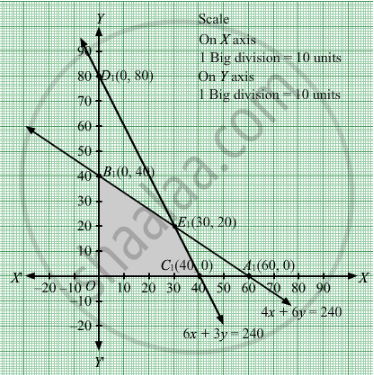
The corner points are C1(40, 0), E1(30, 20) and B1(0, 40).
The values of Z at these corner points are as follows.
| Corner point | Z = 7x + 10y |
| C1(40, 0) | 280 |
| E1(30, 20) | 410 |
| B1(0, 40) | 400 |
The maximum value of Z is 410 at (30, 20).
Thus, the factory should produce 30 packages of screws A and 20 packages of screws B to get the maximum profit of Rs 410.
APPEARS IN
संबंधित प्रश्न
Solve the following L.P.P graphically:
Maximize: Z = 10x + 25y
Subject to: x ≤ 3, y ≤ 3, x + y ≤ 5, x ≥ 0, y ≥ 0
Minimum and maximum z = 5x + 2y subject to the following constraints:
x-2y ≤ 2
3x+2y ≤ 12
-3x+2y ≤ 3
x ≥ 0,y ≥ 0
Solve the following L. P. P. graphically:Linear Programming
Minimize Z = 6x + 2y
Subject to
5x + 9y ≤ 90
x + y ≥ 4
y ≤ 8
x ≥ 0, y ≥ 0
In order to supplement daily diet, a person wishes to take X and Y tablets. The contents (in milligrams per tablet) of iron, calcium and vitamins in X and Y are given as below :
| Tablets | Iron | Calcium | Vitamin |
| x | 6 | 3 | 2 |
| y | 2 | 3 | 4 |
The person needs to supplement at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligrams of vitamins. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each type should the person take in order to satisfy the above requirement at the minimum cost? Make an LPP and solve graphically.
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 3x + 4y
Subject to
\[2x + 2y \leq 80\]
\[2x + 4y \leq 120\]
Minimize Z = 5x + 3y
Subject to
\[2x + y \geq 10\]
\[x + 3y \geq 15\]
\[ x \leq 10\]
\[ y \leq 8\]
\[ x, y \geq 0\]
Minimize Z = x − 5y + 20
Subject to
\[x - y \geq 0\]
\[ - x + 2y \geq 2\]
\[ x \geq 3\]
\[ y \leq 4\]
\[ x, y \geq 0\]
Maximize Z = −x1 + 2x2
Subject to
\[- x_1 + 3 x_2 \leq 10\]
\[ x_1 + x_2 \leq 6\]
\[ x_1 - x_2 \leq 2\]
\[ x_1 , x_2 \geq 0\]
Maximize Z = 3x + 3y, if possible,
Subject to the constraints
\[x - y \leq 1\]
\[x + y \geq 3\]
\[ x, y \geq 0\]
One kind of cake requires 300 gm of flour and 15 gm of fat, another kind of cake requires 150 gm of flour and 30 gm of fat. Find the maximum number of cakes which can be made from 7.5 kg of flour and 600 gm of fat, assuming that there is no shortage of the other ingradients used in making the cake. Make it as an LPP and solve it graphically.
If a young man drives his vehicle at 25 km/hr, he has to spend Rs 2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to Rs 5/per km. He has Rs 100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A small manufacturer has employed 5 skilled men and 10 semi-skilled men and makes an article in two qualities deluxe model and an ordinary model. The making of a deluxe model requires 2 hrs. work by a skilled man and 2 hrs. work by a semi-skilled man. The ordinary model requires 1 hr by a skilled man and 3 hrs. by a semi-skilled man. By union rules no man may work more than 8 hrs per day. The manufacturers clear profit on deluxe model is Rs 15 and on an ordinary model is Rs 10. How many of each type should be made in order to maximize his total daily profit.
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?
A gardener has supply of fertilizer of type I which consists of 10% nitrogen and 6% phosphoric acid and type II fertilizer which consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, he finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for his crop. If the type I fertilizer costs 60 paise per kg and type II fertilizer costs 40 paise per kg, determine how many kilograms of each fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.
A small firm manufacturers items A and B. The total number of items A and B that it can manufacture in a day is at the most 24. Item A takes one hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160, how many of each type of item be produced to maximize the profit? Solve the problem graphically.
A company manufactures two articles A and B. There are two departments through which these articles are processed: (i) assembly and (ii) finishing departments. The maximum capacity of the first department is 60 hours a week and that of other department is 48 hours per week. The product of each unit of article A requires 4 hours in assembly and 2 hours in finishing and that of each unit of B requires 2 hours in assembly and 4 hours in finishing. If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B, find the number of units of A and B to be produced per week in order to have maximum profit.
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weigh 1 kg and \[1\frac{1}{2}\] kg each respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the books of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically.
Tow godowns, A and B, have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal(in Rs.) | ||
| From-> | A | B |
| To | ||
| D | 6.00 | 4.00 |
| E | 3.00 | 2.00 |
| F | 2.50 | 3.00 |
How should the supplies be transported in order that the transportation cost is minimum?
The value of objective function is maximum under linear constraints ______.
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A
require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours and 20 minutes available for cutting and 4 hours available for assembling. The profit is Rs. 50 each for type A and Rs. 60 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize profit? Formulate the above LPP and solve it graphically and also find the maximum profit.
The graph of the inequality 3X − 4Y ≤ 12, X ≤ 1, X ≥ 0, Y ≥ 0 lies in fully in
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
The maximum value of Z = 5x + 4y, Subject to y ≤ 2x, x ≤ 2y, x + y ≤ 3, x ≥ 0, y ≥ 0 is ______.
For the LPP, maximize z = x + 4y subject to the constraints x + 2y ≤ 2, x + 2y ≥ 8, x, y ≥ 0 ______.
The maximum value of z = 3x + 10y subjected to the conditions 5x + 2y ≤ 10, 3x + 5y ≤ 15, x, y ≥ 0 is ______.
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
The minimum value of z = 7x + 9y subject to 3x + y ≤ 6, 5x + 8y ≤ 40, x ≥ 0, y ≥ 2 is ______.
A feasible solution to a linear programming problem
The solution set of the inequality 3x + 5y < 4 is ______.
The corner points of the feasible region of a linear programming problem are (0, 4), (8, 0) and `(20/3, 4/3)`. If Z = 30x + 24y is the objective function, then (maximum value of Z – minimum value of Z) is equal to ______.
Solve the following Linear Programming Problem graphically:
Minimize: Z = 60x + 80y
Subject to constraints:
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
Solve the following Linear Programming Problem graphically.
Maximise Z = 5x + 2y subject to:
x – 2y ≤ 2,
3x + 2y ≤ 12,
– 3x + 2y ≤ 3,
x ≥ 0, y ≥ 0
Aman has ₹ 1500 to purchase rice and wheat for his grocery shop. Each sack of rice and wheat costs ₹ 180 and Rupee ₹ 120 respectively. He can store a maximum number of 10 bags in his shop. He will earn a profit of ₹ 11 per bag of rice and ₹ 9 per bag of wheat.
- Formulate a Linear Programming Problem to maximise Aman’s profit.
- Calculate the maximum profit.
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
