Advertisements
Advertisements
प्रश्न
Two tailors, A and B earn Rs 15 and Rs 20 per day respectively. A can stitch 6 shirts and 4 pants while B can stitch 10 shirts and 4 pants per day. How many days shall each work if it is desired to produce (at least) 60 shirts and 32 pants at a minimum labour cost?
उत्तर
Let tailor A work for x days and tailor B work for y days.
In one day, A can stitch 6 shirts and 4 pants whereas B can stitch 10 shirts and 4 pants
Thus, in x days A can stitch 6x shirts and 4y pants whereas B can stich 10y shirts and 4y pants.
pants.
It is given that the minimum requirement of the shirts and pants are respectively 60 and 32.
Thus,
\[6x + 10y \geq 60\]
\[4x + 4y \geq 32\]
Further it is given that A and B earn Rs 15 and Rs 20 per day respectively.
Thus, A earn Rs 15x and B earn Rs 20y .
Let Z denotes the total cost
\[\therefore Z = 15x + 20y\]
Days cannot be negative.
∴ \[x, y \geq 0\]
Min Z = \[15x + 20y\] subject to
\[6x + 10y \geq 60\]
\[4x + 4y \geq 32\]
6x + 10y = 60, 4x + 4y = 32, x = 0 and y = 0
Region represented by 6x + 10y ≥ 60:
The line 6x + 10y = 60 meets the coordinate axes at A1(10, 0) and B1(0, 6) respectively. By joining these points we obtain the line6x + 10y = 60. Clearly (0,0) does not satisfies the 6x + 10y = 60. So,the region which does not contains the origin represents the solution set of the inequation 6x + 10y ≥ 60.
Region represented by 4x + 4y ≥ 32:
The line 4x + 4y =32 meets the coordinate axes at C1(8, 0) and D1(0, 8) respectively. By joining these points we obtain the line 4x + 4y = 32.Clearly (0,0) does not satisfies the inequation 4x + 4y ≥ 32. So,the region which does not contains the origin represents the solution set of the inequation 4x + 4y ≥ 32.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 6x + 10y ≥ 60,4x + 4y ≥ 32, x ≥ 0, and y ≥ 0 are as follows.
Thus, the mathematical formulation of the given linear programming problem is
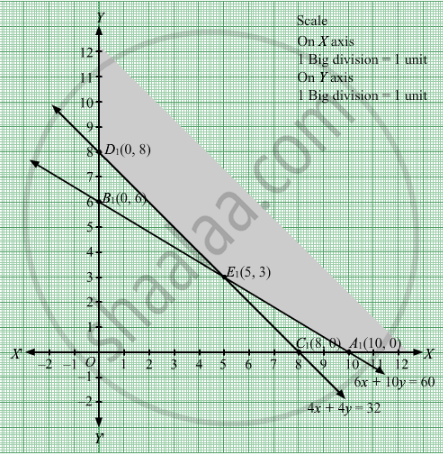The corner points are D1(0, 8), E1(5, 3) and A1(10, 0).The values of Z at these corner points are as follows
| Corner point | Z = 15x + 20y |
| D1 | 160 |
| E1 | 135 |
| A1 | 150 |
The minimum value of Z is 135 which is attained at E1(5, 3).
Thus, for minimum labour cost, A should work for 5 days and B should work for 3 days.
APPEARS IN
संबंधित प्रश्न
Minimize `z=4x+5y ` subject to `2x+y>=7, 2x+3y<=15, x<=3,x>=0, y>=0` solve using graphical method.
A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profits from crops A and B per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximize the total profit? Form an LPP from the above and solve it graphically. Do you agree with the message that the protection of wildlife is utmost necessary to preserve the balance in environment?
Minimize :Z=6x+4y
Subject to : 3x+2y ≥12
x+y ≥5
0 ≤x ≤4
0 ≤ y ≤ 4
A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
Solve the following L. P. P. graphically:Linear Programming
Minimize Z = 6x + 2y
Subject to
5x + 9y ≤ 90
x + y ≥ 4
y ≤ 8
x ≥ 0, y ≥ 0
Maximise Z = x + 2y subject to the constraints
`x + 2y >= 100`
`2x - y <= 0`
`2x + y <= 200`
Solve the above LPP graphically
Maximize Z = 3x + 4y
Subject to
\[2x + 2y \leq 80\]
\[2x + 4y \leq 120\]
Minimize Z = x − 5y + 20
Subject to
\[x - y \geq 0\]
\[ - x + 2y \geq 2\]
\[ x \geq 3\]
\[ y \leq 4\]
\[ x, y \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Find the minimum value of 3x + 5y subject to the constraints
− 2x + y ≤ 4, x + y ≥ 3, x − 2y ≤ 2, x, y ≥ 0.
A manufacturer has three machines installed in his factory. machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day. He produces only two items, each requiring the use of three machines. The number of hours required for producing one unit each of the items on the three machines is given in the following table:
| Item | Number of hours required by the machine | ||
A B |
I | II | III |
| 1 2 |
2 1 |
1 5/4 |
|
He makes a profit of Rs 6.00 on item A and Rs 4.00 on item B. Assuming that he can sell all that he produces, how many of each item should he produces so as to maximize his profit? Determine his maximum profit. Formulate this LPP mathematically and then solve it.
A company produces two types of leather belts, say type A and B. Belt A is a superior quality and belt B is of a lower quality. Profits on each type of belt are Rs 2 and Rs 1.50 per belt, respectively. Each belt of type A requires twice as much time as required by a belt of type B. If all belts were of type B, the company could produce 1000 belts per day. But the supply of leather is sufficient only for 800 belts per day (both A and B combined). Belt A requires a fancy buckle and only 400 fancy buckles are available for this per day. For belt of type B, only 700 buckles are available per day.
How should the company manufacture the two types of belts in order to have a maximum overall profit?
A firm manufacturing two types of electric items, A and B, can make a profit of Rs 20 per unit of A and Rs 30 per unit of B. Each unit of A requires 3 motors and 4 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of these per month is restricted to 210 motors and 300 transformers. Type B is an export model requiring a voltage stabilizer which has a supply restricted to 65 units per month. Formulate the linear programing problem for maximum profit and solve it graphically.
A firm manufactures headache pills in two sizes A and B. Size A contains 2 grains of aspirin, 5 grains of bicarbonate and 1 grain of codeine; size B contains 1 grain of aspirin, 8 grains of bicarbonate and 66 grains of codeine. It has been found by users that it requires at least 12 grains of aspirin, 7.4 grains of bicarbonate and 24 grains of codeine for providing immediate effects. Determine graphically the least number of pills a patient should have to get immediate relief. Determine also the quantity of codeine consumed by patient.
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs 50 each on type A and Rs 60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weigh 1 kg and \[1\frac{1}{2}\] kg each respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the books of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically.
A cooperative society of farmers has 50 hectares of land to grow two crops X and Y. The profits from crops X and Y per hectare are estimated as ₹10,500 and ₹9,000 respectively. To control weeds, a liquid herbicide has to be used for crops X and Y at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. How much land should be allocated to each crop so as to maximise the total profit of the society?
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Types of Toys | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at ₹7 profit and that of B at a profit of ₹4. Find the production level per day for maximum profit graphically.
There are two types of fertilisers 'A' and 'B' . 'A' consists of 12% nitrogen and 5% phosphoric acid whereas 'B' consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If 'A' costs ₹10 per kg and 'B' cost ₹8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requiremnets are met at a minimum cost
Tow godowns, A and B, have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal(in Rs.) | ||
| From-> | A | B |
| To | ||
| D | 6.00 | 4.00 |
| E | 3.00 | 2.00 |
| F | 2.50 | 3.00 |
How should the supplies be transported in order that the transportation cost is minimum?
The value of objective function is maximum under linear constraints ______.
A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.
From the details given below, calculate the five-year moving averages of the number of students who have studied in a school. Also, plot these and original data on the same graph paper.
| Year | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| Number of Students | 332 | 317 | 357 | 392 | 402 | 405 | 410 | 427 | 405 | 438 |
A company manufactures two types of cardigans: type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the company. Solve it graphically and find the maximum profit.
For L.P.P. maximize z = 4x1 + 2x2 subject to 3x1 + 2x2 ≥ 9, x1 - x2 ≤ 3, x1 ≥ 0, x2 ≥ 0 has ______.
The maximum value of Z = 5x + 4y, Subject to y ≤ 2x, x ≤ 2y, x + y ≤ 3, x ≥ 0, y ≥ 0 is ______.
If 4x + 5y ≤ 20, x + y ≥ 3, x ≥ 0, y ≥ 0, maximum 2x + 3y is ______.
The minimum value of z = 7x + 9y subject to 3x + y ≤ 6, 5x + 8y ≤ 40, x ≥ 0, y ≥ 2 is ______.
In linear programming feasible region (or solution region) for the problem is ____________.
Which of the statements describe the solution set for `-2(x + 8) = - 2x + 20`?
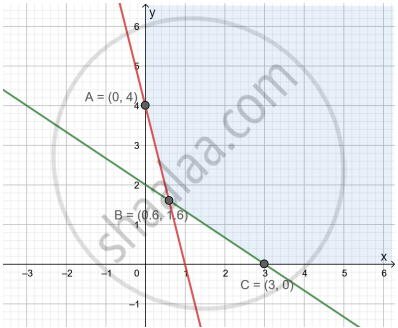
The corner points of the shaded unbounded feasible region of an LPP are (0, 4), (0.6, 1.6) and (3, 0) as shown in the figure. The minimum value of the objective function Z = 4x + 6y occurs at ______.
The constraints –x1 + x2 ≤ 1, –x1 + 3x2 ≤ 9, x1x2 ≥ 0 define on ______.
Solve the following linear programming problem graphically:
Minimize: Z = 5x + 10y
Subject to constraints:
x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
Solve the following Linear Programming problem graphically:
Maximize: Z = 3x + 3.5y
Subject to constraints:
x + 2y ≥ 240,
3x + 1.5y ≥ 270,
1.5x + 2y ≤ 310,
x ≥ 0, y ≥ 0.
