Advertisements
Advertisements
प्रश्न
Solve the following Linear Programming Problem graphically.
Maximise Z = 5x + 2y subject to:
x – 2y ≤ 2,
3x + 2y ≤ 12,
– 3x + 2y ≤ 3,
x ≥ 0, y ≥ 0
उत्तर
Given L.P.P. is
Max. Z = 5x + 2y subject to
x – 2y ≤ 2,
3x + 2y ≤ 12,
– 3x + 2y ≤ 3,
and x ≥ 0, y ≥ 0
First, we draw graphs of lines
x – 2y = 2 ...(1)
3x + 2y = 12 ...(2)
– 3x + 2y = 3 ...(3)
By (1) x – 2y = 2
| x | 2 | 0 |
| y | 0 | – 1 |
A(2, 0) and B(0, – 1)
By (2) 3x + 2y = 12
| x | 4 | 0 |
| y | 0 | 6 |
C(4, 0) and D(0, 6)
By (3) – 3x + 2y = 3
| x | – 1 | 0 |
| y | 0 | 3/2 |
`E(-1, 0), F(0, 3/2)`
Now solving (1) and (2), we get
x = `7/2` and y = `3/4`
Point of intersection `P(7/2, 3/4)`
Solving (2) and (3), we get
x = `3/2`, y = `15/4`
Point of intersection `Q(3/2, 15/4)`
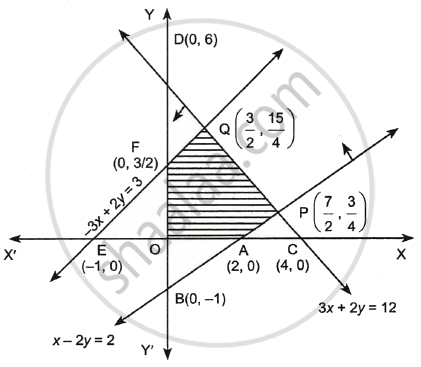
x ≥ 0, y ≥ 0 shows that the shaded region lies in first quadrant.
For x – 2y ≤ 2, take origin (0, 0), then 0 – 0 ≤ 2 which is true.
∴ Shaded the region in which origin lies.
Similarly, we shade the region for various situations.
Hence OAPQFO is the required feasible region.
The corresponding Z values can be evaluated as follows:
| Vertices of shaded region |
Z = 5z + 2y |
| O(0, 0) | Z = 5 × 0 + 2 × 0 = 0 |
| A(2, 0) | Z = 10 + 0 = 10 |
| `P(7/2, 3/4)` | Z = `35/2 + 3/2` = 19 (maximum) |
| `Q(3/2, 15/4)` | Z = `15/2 + 15/2` = 15 |
| `F(0, 3/2)` | Z = 0 + 3 = 3 |
Hence, the maximum value of Z is 19 at the point `P(7/2, 3/4)`.
APPEARS IN
संबंधित प्रश्न
Solve the following LPP by using graphical method.
Maximize : Z = 6x + 4y
Subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Also find maximum value of Z.
Solve the following linear programming problem graphically :
Maximise Z = 7x + 10y subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Solve the following L.P.P. graphically:
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0 and x, y ≥ 0
Solve the following LPP by graphical method:
Minimize Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
Subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Minimize Z = x − 5y + 20
Subject to
\[x - y \geq 0\]
\[ - x + 2y \geq 2\]
\[ x \geq 3\]
\[ y \leq 4\]
\[ x, y \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Solve the following linear programming problem graphically:
Minimize z = 6 x + 3 y
Subject to the constraints:
4 x + \[y \geq\] 80
x + 5 \[y \geq\] 115
3 x + 2 \[y \leq\] 150
\[x \geq\] 0 , \[y \geq\] 0
A hospital dietician wishes to find the cheapest combination of two foods, A and B, that contains at least 0.5 milligram of thiamin and at least 600 calories. Each unit of Acontains 0.12 milligram of thiamin and 100 calories, while each unit of B contains 0.10 milligram of thiamin and 150 calories. If each food costs 10 paise per unit, how many units of each should be combined at a minimum cost?
A wholesale dealer deals in two kinds, A and B (say) of mixture of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew nuts and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew nuts and 180 grams of hazel nuts. The remainder of both mixtures is per nuts. The dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew nuts and 540 grams of hazel nuts. Mixture A costs Rs 8 per kg. and mixture B costs Rs 12 per kg. Assuming that mixtures A and B are uniform, use graphical method to determine the number of kg. of each mixture which he should use to minimise the cost of the bag.
A small manufacturer has employed 5 skilled men and 10 semi-skilled men and makes an article in two qualities deluxe model and an ordinary model. The making of a deluxe model requires 2 hrs. work by a skilled man and 2 hrs. work by a semi-skilled man. The ordinary model requires 1 hr by a skilled man and 3 hrs. by a semi-skilled man. By union rules no man may work more than 8 hrs per day. The manufacturers clear profit on deluxe model is Rs 15 and on an ordinary model is Rs 10. How many of each type should be made in order to maximize his total daily profit.
A furniture manufacturing company plans to make two products : chairs and tables. From its available resources which consists of 400 square feet to teak wood and 450 man hours. It is known that to make a chair requires 5 square feet of wood and 10 man-hours and yields a profit of Rs 45, while each table uses 20 square feet of wood and 25 man-hours and yields a profit of Rs 80. How many items of each product should be produced by the company so that the profit is maximum?
A factory uses three different resources for the manufacture of two different products, 20 units of the resources A, 12 units of B and 16 units of C being available. 1 unit of the first product requires 2, 2 and 4 units of the respective resources and 1 unit of the second product requires 4, 2 and 0 units of respective resources. It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Formulate the linear programming problem. How many units of each product should be manufactured for maximizing the profit? Solve it graphically.
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time.
(i) What number of rackets and bats must be made if the factory is to work at full capacity?
(ii) If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity.
There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds the she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg, determine how much of each type of fertilizer should be used so that the nutrient requirements are met at minimum cost. What is the minimum cost?
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at ₹7 profit and that of B at a profit of ₹4. Find the production level per day for maximum profit graphically.
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
The point at which the maximum value of x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x ≥ 0, y ≥ 0 is obtained, is ______.
The feasible region of an LPP is shown in the figure. If z = 3x + 9y, then the minimum value of z occurs at ______.
The region XOY - plane which is represented by the inequalities -5 ≤ x ≤ 5, -5 ≤ y ≤ 5 is ______
Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at ____________.
In Corner point method for solving a linear programming problem the first step is to ____________.
The comer point of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let x = Px + qx where P, q > 0 condition on P and Q so that the maximum of z occurs at both (3, 4) and (0, 5) is
Solve the following Linear Programming Problem graphically:
Maximize Z = 400x + 300y subject to x + y ≤ 200, x ≤ 40, x ≥ 20, y ≥ 0
The corner points of the feasible region of a linear programming problem are (0, 4), (8, 0) and `(20/3, 4/3)`. If Z = 30x + 24y is the objective function, then (maximum value of Z – minimum value of Z) is equal to ______.
Solve the following Linear Programming Problem graphically:
Minimize: Z = 60x + 80y
Subject to constraints:
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
