Advertisements
Advertisements
प्रश्न
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
उत्तर
Let the number of necklaces manufacture be x,
and the number of bracelets manufacture be y.
since the total number of items are at most 24.
Bracelets takes 1 hour to manufacture and necklaces takes half an hour to manufacture.
x item takes x hour to manufacture and y items take y/2 hour to manufacture.
and maximum time available is 16 hours.
therefore
the profit on one necklace is Rs. 100 and the profit on one bracelet is Rs.300
Let the profit be Z. Now we wish to maximize the profit. So,
Max Z = 100x + 300y ...(3)
So, \[x + y \leq 24\]
Max Z = 100x + 300y is the required L.P.P.
APPEARS IN
संबंधित प्रश्न
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
Find graphically, the maximum value of z = 2x + 5y, subject to constraints given below :
2x + 4y ≤ 83
x + y ≤ 6
x + y ≤ 4
x ≥ 0, y≥ 0
Solve the following L.P.P. graphically Maximise Z = 4x + y
Subject to following constraints x + y ≤ 50
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0
Maximize Z = 5x + 3y
Subject to
\[3x + 5y \leq 15\]
\[5x + 2y \leq 10\]
\[ x, y \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2 are available. Food F1 costs Rs 4 per unit and F2 costs Rs 6 per unit one unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these foods and also meets the mineral nutritional requirements
A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum of vitamin A.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs ₹16 and one kg of food Y costs ₹20. Find the least cost of the mixture which will produce the required diet?
If a young man drives his vehicle at 25 km/hr, he has to spend Rs 2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to Rs 5/per km. He has Rs 100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
Two tailors, A and B earn Rs 15 and Rs 20 per day respectively. A can stitch 6 shirts and 4 pants while B can stitch 10 shirts and 4 pants per day. How many days shall each work if it is desired to produce (at least) 60 shirts and 32 pants at a minimum labour cost?
A firm manufactures headache pills in two sizes A and B. Size A contains 2 grains of aspirin, 5 grains of bicarbonate and 1 grain of codeine; size B contains 1 grain of aspirin, 8 grains of bicarbonate and 66 grains of codeine. It has been found by users that it requires at least 12 grains of aspirin, 7.4 grains of bicarbonate and 24 grains of codeine for providing immediate effects. Determine graphically the least number of pills a patient should have to get immediate relief. Determine also the quantity of codeine consumed by patient.
A company manufactures two types of novelty Souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours available for assembling. The profit is 50 paise each for type A and 60 paise each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A small firm manufacturers items A and B. The total number of items A and B that it can manufacture in a day is at the most 24. Item A takes one hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160, how many of each type of item be produced to maximize the profit? Solve the problem graphically.
A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs 50 each on type A and Rs 60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Make an LPP and solve it graphically.
There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds the she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg, determine how much of each type of fertilizer should be used so that the nutrient requirements are met at minimum cost. What is the minimum cost?
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to product A and product B. Each unit of product A requires 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs. 48 per unit and product B is sold for Rs. 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income? Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A
require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours and 20 minutes available for cutting and 4 hours available for assembling. The profit is Rs. 50 each for type A and Rs. 60 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize profit? Formulate the above LPP and solve it graphically and also find the maximum profit.
A farmer has a supply of chemical fertilizer of type A which contains 10% nitrogen and 6% phosphoric acid and of type B which contains 5% nitrogen and 10% phosphoric acid. After the soil test, it is found that at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The fertilizer of type A costs ₹ 5.00 per kg and the type B costs ₹ 8.00 per kg. Using Linear programming, find how many kilograms of each type of fertilizer should be bought to meet the requirement and for the cost to be minimum. Find the feasible region in the graph.
The graph of the inequality 3X − 4Y ≤ 12, X ≤ 1, X ≥ 0, Y ≥ 0 lies in fully in
The minimum value of z = 10x + 25y subject to 0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≥ 5 is ______.
Area of the region bounded by y = cos x, x = 0, x = π and X-axis is ______ sq.units.
The minimum value of z = 2x + 9y subject to constraints x + y ≥ 1, 2x + 3y ≤ 6, x ≥ 0, y ≥ 0 is ______.
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
For the LPP, maximize z = x + 4y subject to the constraints x + 2y ≤ 2, x + 2y ≥ 8, x, y ≥ 0 ______.
Maximise and Minimise Z = 3x – 4y subject to x – 2y ≤ 0, – 3x + y ≤ 4, x – y ≤ 6, x, y ≥ 0
A feasible region in the set of points which satisfy ____________.
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
The corner points of the bounded feasible region of a LPP are A(0,50), B(20, 40), C(50, 100) and D(0, 200) and the objective function is Z = x + 2y. Then the maximum value is ____________.
A manufacturer wishes to produce two commodities A and B. The number of units of material, labour and equipment needed to produce one unit of each commodity is shown in the table given below. Also shown is the available number of units of each item, material, labour, and equipment.
| Items | Commodity A | Commodity B | Available no. of Units |
| Material | 1 | 2 | 8 |
| Labour | 3 | 2 | 12 |
| Equipment | 1 | 1 | 10 |
Find the maximum profit if each unit of commodity A earns a profit of ₹ 2 and each unit of B earns a profit of ₹ 3.
Minimise z = – 3x + 4y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0 What will be the minimum value of z ?
The corner points of the shaded unbounded feasible region of an LPP are (0, 4), (0.6, 1.6) and (3, 0) as shown in the figure. The minimum value of the objective function Z = 4x + 6y occurs at ______.
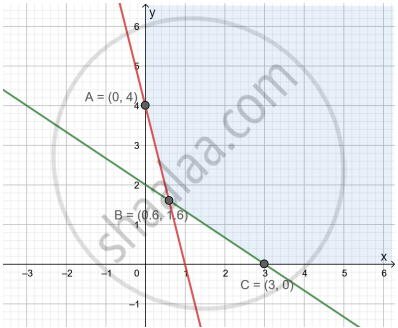
The maximum value of 2x + y subject to 3x + 5y ≤ 26 and 5x + 3y ≤ 30, x ≥ 0, y ≥ 0 is ______.
The objective function Z = ax + by of an LPP has maximum vaiue 42 at (4, 6) and minimum value 19 at (3, 2). Which of the following is true?
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
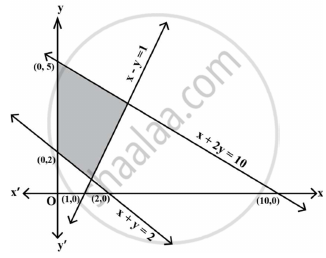
Which of the following is not a constraint to the given Linear Programming Problem?
Minimize z = x + 2y,
Subject to x + 2y ≥ 50, 2x – y ≤ 0, 2x + y ≤ 100, x ≥ 0, y ≥ 0.
Draw the rough graph and shade the feasible region for the inequalities x + y ≥ 2, 2x + y ≤ 8, x ≥ 0, y ≥ 0.
If x – y ≥ 8, x ≥ 3, y ≥ 3, x ≥ 0, y ≥ 0 then find the coordinates of the corner points of the feasible region.
