Advertisements
Advertisements
Question
A factory manufactures two types of screws, A and B, each type requiring the use of two machines - an automatic and a hand-operated. It takes 4 minute on the automatic and 6 minutes on the hand-operated machines to manufacture a package of screws 'A', while it takes 6 minutes on the automatic and 3 minutes on the hand-operated machine to manufacture a package of screws 'B'. Each machine is available for at most 4 hours on any day. The manufacturer can sell a package of screws 'A' at a profit of 70 P and screws 'B' at a profit of Rs 1. Assuming that he can sell all the screws he can manufacture, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
Solution
Let the factory manufacture x screws of type A and y screws of type B on each day. Therefore,
x ≥ 0 and y ≥ 0
The given information can be compiled in a table as follows.
| Screw A | Screw B | Availability | |
| Automatic Machine (min) | 4 | 6 | 4 × 60 = 240 |
| Hand Operated Machine (min) | 6 | 3 | 4 × 60 = 240 |
\[4x + 6y \geq 240\]
The manufacturer can sell a package of screws 'A' at a profit of Rs 0.7 and screws 'B' at a profit of Re 1.
Total profit, Z = 0.7x + 1y
The mathematical formulation of the given problem is
Maximize Z = 0.7x + 1y
subject to the constraints,
x, y ≥ 0
First we will convert inequations into equations as follows:
4x + 6y = 240, 6x + 3y = 240, x = 0 and y = 0
Region represented by 4x + 6y ≤ 240:
The line 4x + 6y = 240 meets the coordinate axes at A1(60, 0) and B1(0, 40) respectively. By joining these points we obtain the line 4x + 6y = 240. Clearly (0,0) satisfies the 4x + 6y = 240. So,the region which contains the origin represents the solution set of the inequation 4x + 6y ≤ 240.
Region represented by 6x + 3y ≤ 240:
The line 6x + 3y = 240 meets the coordinate axes at C1(40, 0) and D1(0, 80) respectively. By joining these points we obtain the line 6x + 3y = 240. Clearly (0,0) satisfies the inequation 6x + 3y ≤ 240. So,the region which contains the origin represents the solution set of the inequation 6x + 3y ≤ 240.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 4x + 6y ≤ 240, 6x + 3y ≤ 240, x ≥ 0, and y ≥ 0 are as follows.
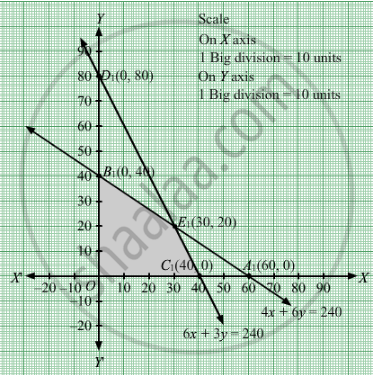
The corner points are C1(40, 0), E1(30, 20) and B1(0, 40).
The values of Z at these corner points are as follows.
| Corner point | Z = 7x + 10y |
| C1(40, 0) | 280 |
| E1(30, 20) | 410 |
| B1(0, 40) | 400 |
The maximum value of Z is 410 at (30, 20).
Thus, the factory should produce 30 packages of screws A and 20 packages of screws B to get the maximum profit of Rs 410.
APPEARS IN
RELATED QUESTIONS
Minimize `z=4x+5y ` subject to `2x+y>=7, 2x+3y<=15, x<=3,x>=0, y>=0` solve using graphical method.
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
A dealer in rural area wishes to purchase a number of sewing machines. He has only Rs 5,760 to invest and has space for at most 20 items for storage. An electronic sewing machine cost him Rs 360 and a manually operated sewing machine Rs 240. He can sell an electronic sewing machine at a profit of Rs 22 and a manually operated sewing machine at a profit of Rs 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit? Make it as a LPP and solve it graphically.
A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profits from crops A and B per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximize the total profit? Form an LPP from the above and solve it graphically. Do you agree with the message that the protection of wildlife is utmost necessary to preserve the balance in environment?
Minimum and maximum z = 5x + 2y subject to the following constraints:
x-2y ≤ 2
3x+2y ≤ 12
-3x+2y ≤ 3
x ≥ 0,y ≥ 0
Find graphically, the maximum value of z = 2x + 5y, subject to constraints given below :
2x + 4y ≤ 83
x + y ≤ 6
x + y ≤ 4
x ≥ 0, y≥ 0
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Maximize Z = 4x + 3y
subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Find the maximum and minimum value of 2x + y subject to the constraints:
x + 3y ≥ 6, x − 3y ≤ 3, 3x + 4y ≤ 24, − 3x + 2y ≤ 6, 5x + y ≥ 5, x, y ≥ 0.
A hospital dietician wishes to find the cheapest combination of two foods, A and B, that contains at least 0.5 milligram of thiamin and at least 600 calories. Each unit of Acontains 0.12 milligram of thiamin and 100 calories, while each unit of B contains 0.10 milligram of thiamin and 150 calories. If each food costs 10 paise per unit, how many units of each should be combined at a minimum cost?
A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum of vitamin A.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 2 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A company produces two types of leather belts, say type A and B. Belt A is a superior quality and belt B is of a lower quality. Profits on each type of belt are Rs 2 and Rs 1.50 per belt, respectively. Each belt of type A requires twice as much time as required by a belt of type B. If all belts were of type B, the company could produce 1000 belts per day. But the supply of leather is sufficient only for 800 belts per day (both A and B combined). Belt A requires a fancy buckle and only 400 fancy buckles are available for this per day. For belt of type B, only 700 buckles are available per day.
How should the company manufacture the two types of belts in order to have a maximum overall profit?
A manufacturer of Furniture makes two products : chairs and tables. processing of these products is done on two machines A and B. A chair requires 2 hrs on machine A and 6 hrs on machine B. A table requires 4 hrs on machine A and 2 hrs on machine B. There are 16 hrs of time per day available on machine A and 30 hrs on machine B. Profit gained by the manufacturer from a chair and a table is Rs 3 and Rs 5 respectively. Find with the help of graph what should be the daily production of each of the two products so as to maximize his profit.
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs 50 each on type A and Rs 60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
A company sells two different products, A and B. The two products are produced in a common production process, which has a total capacity of 500 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of unit of A that can be sold is 70 and that for B is 125. If the profit is Rs 20 per unit for the product A and Rs 15 per unit for the product B, how many units of each product should be sold to maximize profit?
A box manufacturer makes large and small boxes from a large piece of cardboard. The large boxes require 4 sq. metre per box while the small boxes require 3 sq. metre per box. The manufacturer is required to make at least three large boxes and at least twice as many small boxes as large boxes. If 60 sq. metre of cardboard is in stock, and if the profits on the large and small boxes are Rs 3 and Rs 2 per box, how many of each should be made in order to maximize the total profit?
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000.
There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds the she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg, determine how much of each type of fertilizer should be used so that the nutrient requirements are met at minimum cost. What is the minimum cost?
From the details given below, calculate the five-year moving averages of the number of students who have studied in a school. Also, plot these and original data on the same graph paper.
| Year | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| Number of Students | 332 | 317 | 357 | 392 | 402 | 405 | 410 | 427 | 405 | 438 |
The maximum value of z = 6x + 8y subject to x - y ≥ 0, x + 3y ≤ 12, x ≥ 0, y ≥ 0 is ______.
If 4x + 5y ≤ 20, x + y ≥ 3, x ≥ 0, y ≥ 0, maximum 2x + 3y is ______.
In linear programming feasible region (or solution region) for the problem is ____________.
In Corner point method for solving a linear programming problem the first step is to ____________.
The feasible region (shaded) for a L.P.P is shown in the figure. The maximum Z = 5x + 7y is ____________.
A manufacturer wishes to produce two commodities A and B. The number of units of material, labour and equipment needed to produce one unit of each commodity is shown in the table given below. Also shown is the available number of units of each item, material, labour, and equipment.
| Items | Commodity A | Commodity B | Available no. of Units |
| Material | 1 | 2 | 8 |
| Labour | 3 | 2 | 12 |
| Equipment | 1 | 1 | 10 |
Find the maximum profit if each unit of commodity A earns a profit of ₹ 2 and each unit of B earns a profit of ₹ 3.
Minimise z = – 3x + 4y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0 What will be the minimum value of z ?
The corner points of the feasible region of a linear programming problem are (0, 4), (8, 0) and `(20/3, 4/3)`. If Z = 30x + 24y is the objective function, then (maximum value of Z – minimum value of Z) is equal to ______.
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
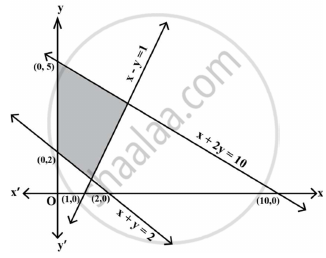
Which of the following is not a constraint to the given Linear Programming Problem?
Solve the following Linear Programming Problem graphically:
Maximize: z = – x + 2y,
Subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Draw the rough graph and shade the feasible region for the inequalities x + y ≥ 2, 2x + y ≤ 8, x ≥ 0, y ≥ 0.
Aman has ₹ 1500 to purchase rice and wheat for his grocery shop. Each sack of rice and wheat costs ₹ 180 and Rupee ₹ 120 respectively. He can store a maximum number of 10 bags in his shop. He will earn a profit of ₹ 11 per bag of rice and ₹ 9 per bag of wheat.
- Formulate a Linear Programming Problem to maximise Aman’s profit.
- Calculate the maximum profit.
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
