Advertisements
Advertisements
Question
A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs 50 each on type A and Rs 60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
Solution
Let x toys of type A and y toys of type B were manufactured.
The given information can be tabulated as follows:
| Cutting time (minutes) | Assembling time (minutes) | |
| Toy A(x) | 5 | 10 |
| Toy B(y) | 8 | 8 |
| Availability | 180 | 240 |
The constraints are
\[5x + 8y \leq 180\]
\[10x + 8y \leq 240\]
The profit is Rs 50 each on type A and Rs 60 each on type B. Therefore, profit gained on x toys of type A and y toys of type B is Rs 50x and Rs 60 y respectively.
Total profit = Z = \[50x + 60y\] The mathematical formulation of the given problem is
Max Z = \[50x + 60y\] subject to
\[5x + 8y \leq 180\]
\[10x + 8y \leq 240\]
First we will convert inequations into equations as follows:
5x + 8y = 180, 10x + 8y = 240, x = 0 and y = 0
Region represented by 5x + 8y ≤ 180:
The line 5x + 8y = 180 meets the coordinate axes at A1(36, 0) and \[B_1 \left( 0, \frac{45}{2} \right)\] respectively. By joining these points we obtain the line 5x + 8y = 180. Clearly, (0,0) satisfies the 5x + 8y = 180. So, the region which contains the origin represents the solution set of the inequation 5x + 8y ≤ 180.
Region represented by 10x + 8y ≤ 240:
The line 10x + 8y = 240 meets the coordinate axes at C1(24, 0) and \[D_1 \left( 0, 30 \right)\] respectively. By joining these points we obtain the line 10x + 8y = 240. Clearly (0,0) satisfies the inequation 10x + 8y ≤ 240. So,the region which contains the origin represents the solution set of the inequation 10x + 8y ≤ 240.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 5x + 8y ≤ 180, 10x + 8y ≤ 240, x ≥ 0 and y ≥ 0 are as follows.
The feasible region is shown in the figure
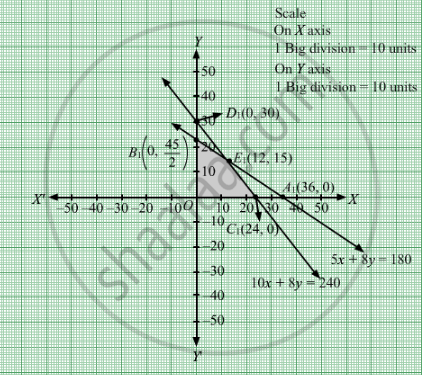The corner points are B1 \[\left( 0, \frac{45}{2} \right)\] E1(12, 15) and C1(24, 0).
The values of Z at the corner points are
| Corner points | Z = \[50x + 60y\] |
| O | 0 |
| B1 | 1350 |
| E1 | 1500 |
| C1 | 1200 |
Thus, for maximum profit, 12 units of toy A and 15 units of toy B should be manufactured.
APPEARS IN
RELATED QUESTIONS
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
Solve the following L.P.P graphically:
Maximize: Z = 10x + 25y
Subject to: x ≤ 3, y ≤ 3, x + y ≤ 5, x ≥ 0, y ≥ 0
A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
Minimum and maximum z = 5x + 2y subject to the following constraints:
x-2y ≤ 2
3x+2y ≤ 12
-3x+2y ≤ 3
x ≥ 0,y ≥ 0
A company manufactures bicycles and tricycles each of which must be processed through machines A and B. Machine A has maximum of 120 hours available and machine B has maximum of 180 hours available. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B.
If profits are Rs. 180 for a bicycle and Rs. 220 for a tricycle, formulate and solve the L.P.P. to determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
Solve the following L. P. P. graphically:Linear Programming
Minimize Z = 6x + 2y
Subject to
5x + 9y ≤ 90
x + y ≥ 4
y ≤ 8
x ≥ 0, y ≥ 0
Solve the following L.P.P. graphically Maximise Z = 4x + y
Subject to following constraints x + y ≤ 50
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Maximize Z = 5x + 3y
Subject to
\[3x + 5y \leq 15\]
\[5x + 2y \leq 10\]
\[ x, y \geq 0\]
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Minimize Z = 30x + 20y
Subject to
\[x + y \leq 8\]
\[ x + 4y \geq 12\]
\[5x + 8y = 20\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
Subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = 3x + 5y
Subject to
\[x + 2y \leq 20\]
\[x + y \leq 15\]
\[ y \leq 5\]
\[ x, y \geq 0\]
Minimize Z = 3x1 + 5x2
Subject to
\[x_1 + 3 x_2 \geq 3\]
\[ x_1 + x_2 \geq 2\]
\[ x_1 , x_2 \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Find the minimum value of 3x + 5y subject to the constraints
− 2x + y ≤ 4, x + y ≥ 3, x − 2y ≤ 2, x, y ≥ 0.
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below:
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 of calories. Two foods A and B, are available at a cost of Rs 4 and Rs 3 per unit respectively. If one unit of A contains 200 units of vitamin, 1 unit of mineral and 40 calories and one unit of food B contains 100 units of vitamin, 2 units of minerals and 40 calories, find what combination of foods should be used to have the least cost?
One kind of cake requires 300 gm of flour and 15 gm of fat, another kind of cake requires 150 gm of flour and 30 gm of fat. Find the maximum number of cakes which can be made from 7.5 kg of flour and 600 gm of fat, assuming that there is no shortage of the other ingradients used in making the cake. Make it as an LPP and solve it graphically.
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 11 units of vitamin B. Food P costs ₹60/kg and food Q costs ₹80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
A company produces two types of leather belts, say type A and B. Belt A is a superior quality and belt B is of a lower quality. Profits on each type of belt are Rs 2 and Rs 1.50 per belt, respectively. Each belt of type A requires twice as much time as required by a belt of type B. If all belts were of type B, the company could produce 1000 belts per day. But the supply of leather is sufficient only for 800 belts per day (both A and B combined). Belt A requires a fancy buckle and only 400 fancy buckles are available for this per day. For belt of type B, only 700 buckles are available per day.
How should the company manufacture the two types of belts in order to have a maximum overall profit?
A firm makes items A and B and the total number of items it can make in a day is 24. It takes one hour to make an item of A and half an hour to make an item of B. The maximum time available per day is 16 hours. The profit on an item of A is Rs 300 and on one item of B is Rs 160. How many items of each type should be produced to maximize the profit? Solve the problem graphically.
A company sells two different products, A and B. The two products are produced in a common production process, which has a total capacity of 500 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of unit of A that can be sold is 70 and that for B is 125. If the profit is Rs 20 per unit for the product A and Rs 15 per unit for the product B, how many units of each product should be sold to maximize profit?
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the number of tennis rackets and cricket bats that the factory must manufacture to earn the maximum profit. Make it as an LPP and solve it graphically.
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A
require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours and 20 minutes available for cutting and 4 hours available for assembling. The profit is Rs. 50 each for type A and Rs. 60 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize profit? Formulate the above LPP and solve it graphically and also find the maximum profit.
Find the graphical solution for the system of linear inequation 2x + y ≤ 2, x − y ≤ 1
Find the feasible solution of linear inequation 2x + 3y ≤ 12, 2x + y ≤ 8, x ≥ 0, y ≥ 0 by graphically
For the LPP, maximize z = x + 4y subject to the constraints x + 2y ≤ 2, x + 2y ≥ 8, x, y ≥ 0 ______.
The point which provides the solution to the linear programming problem: Max P = 2x + 3y subject to constraints: x ≥ 0, y ≥ 0, 2x + 2y ≤ 9, 2x + y ≤ 7, x + 2y ≤ 8, is ______
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is ______.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then ____________.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
In the Corner point method for solving a linear programming problem the second step after finding the feasible region of the linear programming problem and determining its corner points is ____________.
The objective function Z = x1 + x2, subject to the constraints are x1 + x2 ≤ 10, – 2x1 + 3x2 ≤ 15, x1 ≤ 6, x1, x2 ≥ 0, has maximum value ______ of the feasible region.
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
Solve the following Linear Programming Problem graphically:
Minimize: Z = 60x + 80y
Subject to constraints:
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
Solve the following Linear Programming Problem graphically:
Maximize: z = – x + 2y,
Subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Find feasible solution for the following system of linear inequation graphically.
3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
