Advertisements
Advertisements
प्रश्न
A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs 50 each on type A and Rs 60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
उत्तर
Let x toys of type A and y toys of type B were manufactured.
The given information can be tabulated as follows:
| Cutting time (minutes) | Assembling time (minutes) | |
| Toy A(x) | 5 | 10 |
| Toy B(y) | 8 | 8 |
| Availability | 180 | 240 |
The constraints are
\[5x + 8y \leq 180\]
\[10x + 8y \leq 240\]
The profit is Rs 50 each on type A and Rs 60 each on type B. Therefore, profit gained on x toys of type A and y toys of type B is Rs 50x and Rs 60 y respectively.
Total profit = Z = \[50x + 60y\] The mathematical formulation of the given problem is
Max Z = \[50x + 60y\] subject to
\[5x + 8y \leq 180\]
\[10x + 8y \leq 240\]
First we will convert inequations into equations as follows:
5x + 8y = 180, 10x + 8y = 240, x = 0 and y = 0
Region represented by 5x + 8y ≤ 180:
The line 5x + 8y = 180 meets the coordinate axes at A1(36, 0) and \[B_1 \left( 0, \frac{45}{2} \right)\] respectively. By joining these points we obtain the line 5x + 8y = 180. Clearly, (0,0) satisfies the 5x + 8y = 180. So, the region which contains the origin represents the solution set of the inequation 5x + 8y ≤ 180.
Region represented by 10x + 8y ≤ 240:
The line 10x + 8y = 240 meets the coordinate axes at C1(24, 0) and \[D_1 \left( 0, 30 \right)\] respectively. By joining these points we obtain the line 10x + 8y = 240. Clearly (0,0) satisfies the inequation 10x + 8y ≤ 240. So,the region which contains the origin represents the solution set of the inequation 10x + 8y ≤ 240.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 5x + 8y ≤ 180, 10x + 8y ≤ 240, x ≥ 0 and y ≥ 0 are as follows.
The feasible region is shown in the figure
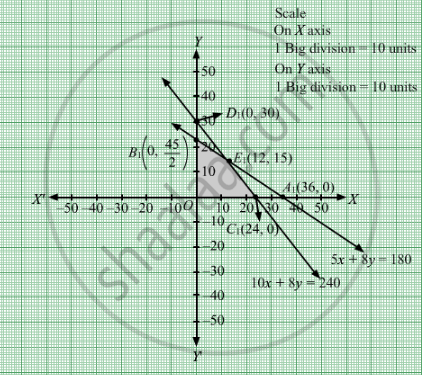The corner points are B1 \[\left( 0, \frac{45}{2} \right)\] E1(12, 15) and C1(24, 0).
The values of Z at the corner points are
| Corner points | Z = \[50x + 60y\] |
| O | 0 |
| B1 | 1350 |
| E1 | 1500 |
| C1 | 1200 |
Thus, for maximum profit, 12 units of toy A and 15 units of toy B should be manufactured.
APPEARS IN
संबंधित प्रश्न
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
Solve the following LPP by using graphical method.
Maximize : Z = 6x + 4y
Subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Also find maximum value of Z.
Solve the following L.P.P. graphically:
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0 and x, y ≥ 0
Maximize Z = 5x + 3y
Subject to
\[3x + 5y \leq 15\]
\[5x + 2y \leq 10\]
\[ x, y \geq 0\]
Maximize Z = 9x + 3y
Subject to
\[2x + 3y \leq 13\]
\[ 3x + y \leq 5\]
\[ x, y \geq 0\]
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = 10x + 6y
Subject to
\[3x + y \leq 12\]
\[2x + 5y \leq 34\]
\[ x, y \geq 0\]
Minimize Z = 2x + 4y
Subject to
\[x + y \geq 8\]
\[x + 4y \geq 12\]
\[x \geq 3, y \geq 2\]
Maximize Z = 2x + 3y
Subject to
\[x + y \geq 1\]
\[10x + y \geq 5\]
\[x + 10y \geq 1\]
\[ x, y \geq 0\]
Find the maximum and minimum value of 2x + y subject to the constraints:
x + 3y ≥ 6, x − 3y ≤ 3, 3x + 4y ≤ 24, − 3x + 2y ≤ 6, 5x + y ≥ 5, x, y ≥ 0.
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no storage of the other ingredients used in making the cakes.
If a young man drives his vehicle at 25 km/hr, he has to spend Rs 2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to Rs 5/per km. He has Rs 100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A firm manufactures two products A and B. Each product is processed on two machines M1 and M2. Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2. The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs 3 and Rs 4 respectively.
Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
A gardener has supply of fertilizer of type I which consists of 10% nitrogen and 6% phosphoric acid and type II fertilizer which consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, he finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for his crop. If the type I fertilizer costs 60 paise per kg and type II fertilizer costs 40 paise per kg, determine how many kilograms of each fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.
A manufacturing company makes two models A and B of a product. Each piece of model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of ₹8000 on each piece of model A and ₹12000 on each piece of model B. How many pieces of model A and model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
| From \ To | Cost (in ₹) | ||
| A | B | C | |
| P | 160 | 100 | 150 |
| Q | 100 | 120 | 100 |
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?
Maximize: z = 3x + 5y Subject to
x +4y ≤ 24 3x + y ≤ 21
x + y ≤ 9 x ≥ 0 , y ≥0
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to product A and product B. Each unit of product A requires 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs. 48 per unit and product B is sold for Rs. 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income? Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.
From the details given below, calculate the five-year moving averages of the number of students who have studied in a school. Also, plot these and original data on the same graph paper.
| Year | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| Number of Students | 332 | 317 | 357 | 392 | 402 | 405 | 410 | 427 | 405 | 438 |
A company manufactures two types of cardigans: type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the company. Solve it graphically and find the maximum profit.
Sketch the graph of inequation x ≥ 5y in xoy co-ordinate system
Find the graphical solution for the system of linear inequation 2x + y ≤ 2, x − y ≤ 1
The maximum value of Z = 5x + 4y, Subject to y ≤ 2x, x ≤ 2y, x + y ≤ 3, x ≥ 0, y ≥ 0 is ______.
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
The maximum value of z = 3x + 10y subjected to the conditions 5x + 2y ≤ 10, 3x + 5y ≤ 15, x, y ≥ 0 is ______.
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of an L.P.P. is called its ____________.
In linear programming feasible region (or solution region) for the problem is ____________.
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
A manufacturer wishes to produce two commodities A and B. The number of units of material, labour and equipment needed to produce one unit of each commodity is shown in the table given below. Also shown is the available number of units of each item, material, labour, and equipment.
| Items | Commodity A | Commodity B | Available no. of Units |
| Material | 1 | 2 | 8 |
| Labour | 3 | 2 | 12 |
| Equipment | 1 | 1 | 10 |
Find the maximum profit if each unit of commodity A earns a profit of ₹ 2 and each unit of B earns a profit of ₹ 3.
The comer point of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let x = Px + qx where P, q > 0 condition on P and Q so that the maximum of z occurs at both (3, 4) and (0, 5) is
The shaded part of given figure indicates in feasible region, then the constraints are:
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
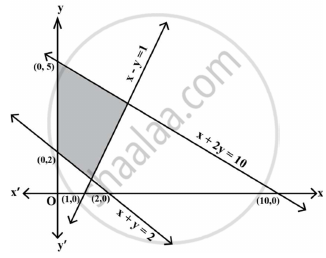
Which of the following is not a constraint to the given Linear Programming Problem?
If x – y ≥ 8, x ≥ 3, y ≥ 3, x ≥ 0, y ≥ 0 then find the coordinates of the corner points of the feasible region.
