Advertisements
Advertisements
प्रश्न
Maximize Z = 9x + 3y
Subject to
\[2x + 3y \leq 13\]
\[ 3x + y \leq 5\]
\[ x, y \geq 0\]
उत्तर
First, we will convert the given inequations into equations, we obtain the following equations:
2x + 3y = 13, 3x +y = 5, x = 0 and y = 0
Region represented by 2x + 3y ≤ 13 :
The line 2x + 3y = 13 meets the coordinate axes at \[A\left( \frac{13}{2}, 0 \right)\] and \[B\left( 0, \frac{13}{3} \right)\] respectively. By joining these points we obtain the line 2x + 3y = 13.
Region represented by 3x + y ≤ 5:
The line 5x + 2y = 10 meets the coordinate axes at
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints, 2x + 3y ≤ 13, 3x + y ≤ 5, x ≥ 0, and y ≥ 0, are as follows.

The corner points of the feasible region are O(0, 0),
The values of Z at these corner points are as follows.
We see that the maximum value of the objective function Z is 15 which is at C
| Corner point | Z = 9x + 3y |
| O(0, 0) | 9 × 0 + 3 × 0 = 0 |
|
\[C\left( \frac{5}{3}, 0 \right)\]
|
9 × \[\frac{5}{3}\] + 3 × 0 =15 |
|
\[E\left( \frac{2}{7}, \frac{29}{7} \right)\]
|
9 × \[\frac{2}{7}\] +3 × \[\frac{29}{7}\] = 15
|
|
\[B\left( 0, \frac{13}{3} \right)\]
|
9 × 0 +3 × \[\frac{13}{3}\] = 113
|
APPEARS IN
संबंधित प्रश्न
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
Solve the following linear programming problem graphically :
Maximise Z = 7x + 10y subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Solve the following LPP by graphical method:
Minimize Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Maximize Z = 4x + 3y
subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = 15x + 10y
Subject to
\[3x + 2y \leq 80\]
\[2x + 3y \leq 70\]
\[ x, y \geq 0\]
Maximize Z = 10x + 6y
Subject to
\[3x + y \leq 12\]
\[2x + 5y \leq 34\]
\[ x, y \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Solve the following LPP graphically:
Maximize Z = 20 x + 10 y
Subject to the following constraints
\[x +\]2\[y \leq\]28
3x+ \[y \leq\]24
\[x \geq\] 2x.
\[y \geq\] 0
A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 of calories. Two foods A and B, are available at a cost of Rs 4 and Rs 3 per unit respectively. If one unit of A contains 200 units of vitamin, 1 unit of mineral and 40 calories and one unit of food B contains 100 units of vitamin, 2 units of minerals and 40 calories, find what combination of foods should be used to have the least cost?
A small manufacturer has employed 5 skilled men and 10 semi-skilled men and makes an article in two qualities deluxe model and an ordinary model. The making of a deluxe model requires 2 hrs. work by a skilled man and 2 hrs. work by a semi-skilled man. The ordinary model requires 1 hr by a skilled man and 3 hrs. by a semi-skilled man. By union rules no man may work more than 8 hrs per day. The manufacturers clear profit on deluxe model is Rs 15 and on an ordinary model is Rs 10. How many of each type should be made in order to maximize his total daily profit.
A manufacturer makes two types A and B of tea-cups. Three machines are needed for the manufacture and the time in minutes required for each cup on the machines is given below:
| Machines | |||
| I | II | III | |
| A B |
12 6 |
18 0 |
6 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each cup A is 75 paise and that on each cup B is 50 paise, show that 15 tea-cups of type A and 30 of type B should be manufactured in a day to get the maximum profit.
A manufacturer of Furniture makes two products : chairs and tables. processing of these products is done on two machines A and B. A chair requires 2 hrs on machine A and 6 hrs on machine B. A table requires 4 hrs on machine A and 2 hrs on machine B. There are 16 hrs of time per day available on machine A and 30 hrs on machine B. Profit gained by the manufacturer from a chair and a table is Rs 3 and Rs 5 respectively. Find with the help of graph what should be the daily production of each of the two products so as to maximize his profit.
A firm manufactures two products A and B. Each product is processed on two machines M1 and M2. Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2. The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs 3 and Rs 4 respectively.
Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
A factory uses three different resources for the manufacture of two different products, 20 units of the resources A, 12 units of B and 16 units of C being available. 1 unit of the first product requires 2, 2 and 4 units of the respective resources and 1 unit of the second product requires 4, 2 and 0 units of respective resources. It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Formulate the linear programming problem. How many units of each product should be manufactured for maximizing the profit? Solve it graphically.
A firm manufactures headache pills in two sizes A and B. Size A contains 2 grains of aspirin, 5 grains of bicarbonate and 1 grain of codeine; size B contains 1 grain of aspirin, 8 grains of bicarbonate and 66 grains of codeine. It has been found by users that it requires at least 12 grains of aspirin, 7.4 grains of bicarbonate and 24 grains of codeine for providing immediate effects. Determine graphically the least number of pills a patient should have to get immediate relief. Determine also the quantity of codeine consumed by patient.
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Make an LPP and solve it graphically.
There are two types of fertilisers 'A' and 'B' . 'A' consists of 12% nitrogen and 5% phosphoric acid whereas 'B' consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If 'A' costs ₹10 per kg and 'B' cost ₹8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requiremnets are met at a minimum cost
The point at which the maximum value of x + y subject to the constraints x + 2y ≤ 70, 2x + y ≤ 95, x ≥ 0, y ≥ 0 is obtained, is ______.
A farmer has a supply of chemical fertilizer of type A which contains 10% nitrogen and 6% phosphoric acid and of type B which contains 5% nitrogen and 10% phosphoric acid. After the soil test, it is found that at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The fertilizer of type A costs ₹ 5.00 per kg and the type B costs ₹ 8.00 per kg. Using Linear programming, find how many kilograms of each type of fertilizer should be bought to meet the requirement and for the cost to be minimum. Find the feasible region in the graph.
From the details given below, calculate the five-year moving averages of the number of students who have studied in a school. Also, plot these and original data on the same graph paper.
| Year | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| Number of Students | 332 | 317 | 357 | 392 | 402 | 405 | 410 | 427 | 405 | 438 |
A company manufactures two types of cardigans: type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the company. Solve it graphically and find the maximum profit.
Find the feasible solution of linear inequation 2x + 3y ≤ 12, 2x + y ≤ 8, x ≥ 0, y ≥ 0 by graphically
The minimum value of z = 10x + 25y subject to 0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≥ 5 is ______.
The minimum value of z = 2x + 9y subject to constraints x + y ≥ 1, 2x + 3y ≤ 6, x ≥ 0, y ≥ 0 is ______.
The minimum value of z = 7x + 9y subject to 3x + y ≤ 6, 5x + 8y ≤ 40, x ≥ 0, y ≥ 2 is ______.
Which of the statements describe the solution set for `-2(x + 8) = - 2x + 20`?
The comer point of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let x = Px + qx where P, q > 0 condition on P and Q so that the maximum of z occurs at both (3, 4) and (0, 5) is
The constraints –x1 + x2 ≤ 1, –x1 + 3x2 ≤ 9, x1x2 ≥ 0 define on ______.
The corner points of the feasible region of a linear programming problem are (0, 4), (8, 0) and `(20/3, 4/3)`. If Z = 30x + 24y is the objective function, then (maximum value of Z – minimum value of Z) is equal to ______.
Solve the following linear programming problem graphically:
Minimize: Z = 5x + 10y
Subject to constraints:
x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
Solve the following Linear Programming problem graphically:
Maximize: Z = 3x + 3.5y
Subject to constraints:
x + 2y ≥ 240,
3x + 1.5y ≥ 270,
1.5x + 2y ≤ 310,
x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problem graphically:
Minimize: Z = 60x + 80y
Subject to constraints:
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
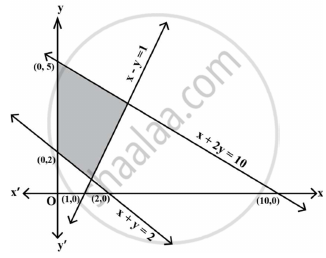
Which of the following is not a constraint to the given Linear Programming Problem?
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
