Advertisements
Advertisements
प्रश्न
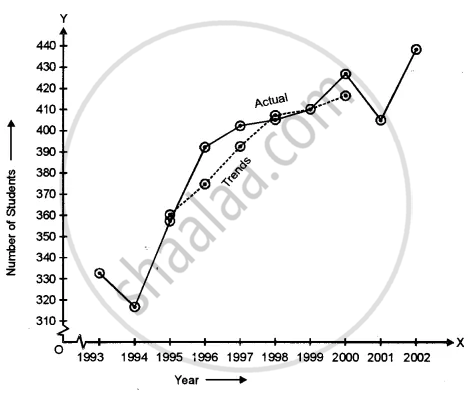
From the details given below, calculate the five-year moving averages of the number of students who have studied in a school. Also, plot these and original data on the same graph paper.
| Year | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 |
| Number of Students | 332 | 317 | 357 | 392 | 402 | 405 | 410 | 427 | 405 | 438 |
उत्तर
| Year | Number of Students | 5 year moving total | 5-year moving average |
|
1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 |
332 317 357 392 402 405 410 427 405 438 |
- - 1800 1873 1966 2036 2049 2085 - - |
- - 360.00 374.60 393.20 407.20 409.80 417.00 - - |
APPEARS IN
संबंधित प्रश्न
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
A company manufactures bicycles and tricycles each of which must be processed through machines A and B. Machine A has maximum of 120 hours available and machine B has maximum of 180 hours available. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B.
If profits are Rs. 180 for a bicycle and Rs. 220 for a tricycle, formulate and solve the L.P.P. to determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
Solve the following L.P.P. graphically Maximise Z = 4x + y
Subject to following constraints x + y ≤ 50
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0
Solve the following L.P.P graphically: Maximise Z = 20x + 10y
Subject to the following constraints x + 2y ≤ 28,
3x + y ≤ 24,
x ≥ 2,
x, y ≥ 0
In order to supplement daily diet, a person wishes to take X and Y tablets. The contents (in milligrams per tablet) of iron, calcium and vitamins in X and Y are given as below :
| Tablets | Iron | Calcium | Vitamin |
| x | 6 | 3 | 2 |
| y | 2 | 3 | 4 |
The person needs to supplement at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligrams of vitamins. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each type should the person take in order to satisfy the above requirement at the minimum cost? Make an LPP and solve graphically.
Minimize Z = x − 5y + 20
Subject to
\[x - y \geq 0\]
\[ - x + 2y \geq 2\]
\[ x \geq 3\]
\[ y \leq 4\]
\[ x, y \geq 0\]
Maximize Z = 3x + 3y, if possible,
Subject to the constraints
\[x - y \leq 1\]
\[x + y \geq 3\]
\[ x, y \geq 0\]
Solve the following LPP graphically:
Maximize Z = 20 x + 10 y
Subject to the following constraints
\[x +\]2\[y \leq\]28
3x+ \[y \leq\]24
\[x \geq\] 2x.
\[y \geq\] 0
Kellogg is a new cereal formed of a mixture of bran and rice that contains at least 88 grams of protein and at least 36 milligrams of iron. Knowing that bran contains 80 grams of protein and 40 milligrams of iron per kilogram, and that rice contains 100 grams of protein and 30 milligrams of iron per kilogram, find the minimum cost of producing this new cereal if bran costs Rs 5 per kg and rice costs Rs 4 per kg
A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum of vitamin A.
If a young man drives his vehicle at 25 km/hr, he has to spend Rs 2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to Rs 5/per km. He has Rs 100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats of first class. However, at least 4 times as many passengers prefer to travel by economy class to the first class. Determine how many each type of tickets must be sold in order to maximize the profit for the airline. What is the maximum profit.
A box manufacturer makes large and small boxes from a large piece of cardboard. The large boxes require 4 sq. metre per box while the small boxes require 3 sq. metre per box. The manufacturer is required to make at least three large boxes and at least twice as many small boxes as large boxes. If 60 sq. metre of cardboard is in stock, and if the profits on the large and small boxes are Rs 3 and Rs 2 per box, how many of each should be made in order to maximize the total profit?
An oil company has two depots, A and B, with capacities of 7000 litres and 4000 litres respectively. The company is to supply oil to three petrol pumps, D, E, F whose requirements are 4500, 3000 and 3500 litres respectively. The distance (in km) between the depots and petrol pumps is given in the following table:
Figure
Assuming that the transportation cost per km is Rs 1.00 per litre, how should the delivery be scheduled in order that the transportation cost is minimum?
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Make an LPP and solve it graphically.
A cooperative society of farmers has 50 hectares of land to grow two crops X and Y. The profits from crops X and Y per hectare are estimated as ₹10,500 and ₹9,000 respectively. To control weeds, a liquid herbicide has to be used for crops X and Y at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. How much land should be allocated to each crop so as to maximise the total profit of the society?
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000.
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Types of Toys | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A
require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours and 20 minutes available for cutting and 4 hours available for assembling. The profit is Rs. 50 each for type A and Rs. 60 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize profit? Formulate the above LPP and solve it graphically and also find the maximum profit.
The region XOY - plane which is represented by the inequalities -5 ≤ x ≤ 5, -5 ≤ y ≤ 5 is ______
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of an L.P.P. is called its ____________.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
In Corner point method for solving a linear programming problem the first step is to ____________.
In the Corner point method for solving a linear programming problem the second step after finding the feasible region of the linear programming problem and determining its corner points is ____________.
Any point in the feasible region that gives the optional value (maximum or minimum) of the objective function is called:-
The objective function Z = x1 + x2, subject to the constraints are x1 + x2 ≤ 10, – 2x1 + 3x2 ≤ 15, x1 ≤ 6, x1, x2 ≥ 0, has maximum value ______ of the feasible region.
Solve the following linear programming problem graphically:
Maximize: Z = x + 2y
Subject to constraints:
x + 2y ≥ 100,
2x – y ≤ 0
2x + y ≤ 200,
x ≥ 0, y ≥ 0.
Minimize z = x + 2y,
Subject to x + 2y ≥ 50, 2x – y ≤ 0, 2x + y ≤ 100, x ≥ 0, y ≥ 0.
