Advertisements
Advertisements
प्रश्न
If a young man drives his vehicle at 25 km/hr, he has to spend Rs 2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to Rs 5/per km. He has Rs 100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
उत्तर
Let young man drives x km at a speed of 25 km/hr and y km at a speed of \[40 km/hr\] Clearly, \[x, y \geq 0\]
It is given that, he spends Rs 2 per km if he drives at a speed of \[25 km/hr\] and Rs 5 per km if he drives at a speed of \[40 km/hr\] . Therefore, money spent by him when he travelled x km and y km is Rs 2x and Rs 5y respectively.
It is given that he has a maximum of Rs 100 to spend.
Thus, \[2x + 5y \leq 100\]
\[\text{ Time spent by him when travelling with a speed of 25 km/hr } = \frac{x}{25}hr\]
\[\text{ Time spent by him when travelling with a speed of 40 km/hr} = \frac{x}{40}hr\]
Also, the available time is of 1 hour.
\[\frac{x}{25} + \frac{y}{40} \leq 1\]
\[ \Rightarrow 40x + 25y \leq 1000\]
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = \[x + y\]
\[2x + 5y \leq 100\]
\[40x + 25y \leq 1000\]
2x + 5y = 100, 40x + 25y = 1000, x = 0 and y = 0
Region represented by 2x + 5y ≤ 100:
The line 2x + 5y = 100 meets the coordinate axes at \[A\left( 50, 0 \right)\] and \[B\left( 0, 20 \right)\] respectively. By joining these points we obtain the line 2x + 5y = 100. Clearly (0,0) satisfies the 2x + 5y = 100. So,the region which contains the origin represents the solution set of the inequation 2x + 5y ≤ 100.
Region represented by 40x + 25y ≤ 1000:
The line 40x + 25y = 1000 meets the coordinate axes at
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 5y ≤ 100, 40x + 25y ≤ 1000, x ≥ 0, and y ≥ 0 are as follows
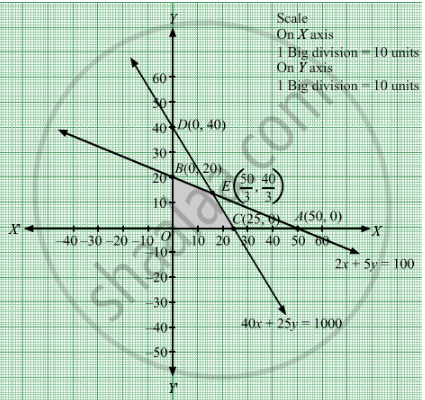The corner points are O(0, 0), B(0, 20),
The values of Z at these corner points are as follows
| Corner point | Z = x + y |
| O | 0 |
| B | 20 |
| E | 30 |
| C | 25 |
The maximum value of Z is 30 which is attained at E.
Thus, the maximum distance travelled by the young man is 30 kms, if he drives
APPEARS IN
संबंधित प्रश्न
A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profits from crops A and B per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximize the total profit? Form an LPP from the above and solve it graphically. Do you agree with the message that the protection of wildlife is utmost necessary to preserve the balance in environment?
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs 7 profit and B at a profit of Rs 4. Find the production level per day for maximum profit graphically.
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y
Subject to: x + 4y ≤ 24
3x + y ≤ 21
x + y ≤ 9
x ≥ 0, y ≥ 0
Solve the following L. P. P. graphically:Linear Programming
Minimize Z = 6x + 2y
Subject to
5x + 9y ≤ 90
x + y ≥ 4
y ≤ 8
x ≥ 0, y ≥ 0
A dietician wishes to mix two kinds ·of food X· and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B arid 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin.B | Vitamin C |
| X | 1 unit | 2 unit | 3 unit |
| Y | 2 unit | 2 unit | 1 unit |
Orie kg of food X costs Rs 24 and one kg of food Y costs Rs 36. Using Linear Programming, find the least cost of the total mixture. which will contain the required vitamins.
Minimize Z = x − 5y + 20
Subject to
\[x - y \geq 0\]
\[ - x + 2y \geq 2\]
\[ x \geq 3\]
\[ y \leq 4\]
\[ x, y \geq 0\]
Maximize Z = 2x + 3y
Subject to
\[x + y \geq 1\]
\[10x + y \geq 5\]
\[x + 10y \geq 1\]
\[ x, y \geq 0\]
Find the minimum value of 3x + 5y subject to the constraints
− 2x + y ≤ 4, x + y ≥ 3, x − 2y ≤ 2, x, y ≥ 0.
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below:
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
A wholesale dealer deals in two kinds, A and B (say) of mixture of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew nuts and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew nuts and 180 grams of hazel nuts. The remainder of both mixtures is per nuts. The dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew nuts and 540 grams of hazel nuts. Mixture A costs Rs 8 per kg. and mixture B costs Rs 12 per kg. Assuming that mixtures A and B are uniform, use graphical method to determine the number of kg. of each mixture which he should use to minimise the cost of the bag.
A manufacturer has three machines installed in his factory. machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day. He produces only two items, each requiring the use of three machines. The number of hours required for producing one unit each of the items on the three machines is given in the following table:
| Item | Number of hours required by the machine | ||
A B |
I | II | III |
| 1 2 |
2 1 |
1 5/4 |
|
He makes a profit of Rs 6.00 on item A and Rs 4.00 on item B. Assuming that he can sell all that he produces, how many of each item should he produces so as to maximize his profit? Determine his maximum profit. Formulate this LPP mathematically and then solve it.
A company produces two types of leather belts, say type A and B. Belt A is a superior quality and belt B is of a lower quality. Profits on each type of belt are Rs 2 and Rs 1.50 per belt, respectively. Each belt of type A requires twice as much time as required by a belt of type B. If all belts were of type B, the company could produce 1000 belts per day. But the supply of leather is sufficient only for 800 belts per day (both A and B combined). Belt A requires a fancy buckle and only 400 fancy buckles are available for this per day. For belt of type B, only 700 buckles are available per day.
How should the company manufacture the two types of belts in order to have a maximum overall profit?
A chemical company produces two compounds, A and B. The following table gives the units of ingredients, C and D per kg of compounds A and B as well as minimum requirements of C and D and costs per kg of A and B. Find the quantities of A and B which would give a supply of C and D at a minimum cost.
| Compound | Minimum requirement | ||
| A | B | ||
| Ingredient C Ingredient D |
1 3 |
2 1 |
80 75 |
| Cost (in Rs) per kg | 4 | 6 | - |
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
A manufacturer of patent medicines is preparing a production plan on medicines, A and B. There are sufficient raw materials available to make 20000 bottles of A and 40000 bottles of B, but there are only 45000 bottles into which either of the medicines can be put. Further, it takes 3 hours to prepare enough material to fill 1000 bottles of A, it takes 1 hour to prepare enough material to fill 1000 bottles of B and there are 66 hours available for this operation. The profit is Rs 8 per bottle for A and Rs 7 per bottle for B. How should the manufacturer schedule his production in order to maximize his profit?
Anil wants to invest at most Rs 12000 in Saving Certificates and National Saving Bonds. According to rules, he has to invest at least Rs 2000 in Saving Certificates and at least Rs 4000 in National Saving Bonds. If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bond is 10% per annum, how much money should he invest to earn maximum yearly income? Find also his maximum yearly income.
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.
If a young man drives his vehicle at 25 km/hr, he has to spend ₹2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to ₹5 per km. He has ₹100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is at most 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs 300 and that on a chain is Rs 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an LPP and solve it graphically.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Make an LPP and solve it graphically.
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
Tow godowns, A and B, have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal(in Rs.) | ||
| From-> | A | B |
| To | ||
| D | 6.00 | 4.00 |
| E | 3.00 | 2.00 |
| F | 2.50 | 3.00 |
How should the supplies be transported in order that the transportation cost is minimum?
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to product A and product B. Each unit of product A requires 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs. 48 per unit and product B is sold for Rs. 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income? Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
Find the solution set of inequalities 0 ≤ x ≤ 5, 0 ≤ 2y ≤ 7
The region XOY - plane which is represented by the inequalities -5 ≤ x ≤ 5, -5 ≤ y ≤ 5 is ______
The maximum value of z = 3x + 10y subjected to the conditions 5x + 2y ≤ 10, 3x + 5y ≤ 15, x, y ≥ 0 is ______.
Of all the points of the feasible region for maximum or minimum of objective function the points.
Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at ____________.
In linear programming feasible region (or solution region) for the problem is ____________.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and ____________.
A feasible solution to a linear programming problem
The feasible region (shaded) for a L.P.P is shown in the figure. The maximum Z = 5x + 7y is ____________.
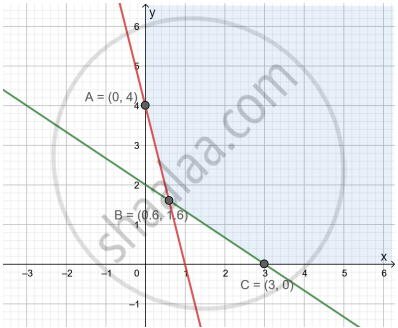
The corner points of the shaded unbounded feasible region of an LPP are (0, 4), (0.6, 1.6) and (3, 0) as shown in the figure. The minimum value of the objective function Z = 4x + 6y occurs at ______.
The maximum value of 2x + y subject to 3x + 5y ≤ 26 and 5x + 3y ≤ 30, x ≥ 0, y ≥ 0 is ______.
The objective function Z = x1 + x2, subject to the constraints are x1 + x2 ≤ 10, – 2x1 + 3x2 ≤ 15, x1 ≤ 6, x1, x2 ≥ 0, has maximum value ______ of the feasible region.
Minimize z = x + 2y,
Subject to x + 2y ≥ 50, 2x – y ≤ 0, 2x + y ≤ 100, x ≥ 0, y ≥ 0.
If x – y ≥ 8, x ≥ 3, y ≥ 3, x ≥ 0, y ≥ 0 then find the coordinates of the corner points of the feasible region.
