Advertisements
Advertisements
प्रश्न
A small firm manufactures gold rings and chains. The total number of rings and chains manufactured per day is at most 24. It takes 1 hour to make a ring and 30 minutes to make a chain. The maximum number of hours available per day is 16. If the profit on a ring is Rs 300 and that on a chain is Rs 190, find the number of rings and chains that should be manufactured per day, so as to earn the maximum profit. Make it as an LPP and solve it graphically.
उत्तर
Let the firm manufacture x gold rings and y chains per day.
Number of gold rings and chains cannot be negative.
Therefore, x ≥0 and y ≥0.
It is given that the total number of gold rings and chains manufactured per day is at most 24.
∴ x + y ≤ 24
The gold ring takes 1 hour to make and chain takes 30 min, that is, 0.5 hour to make.
The maximum number of hours available per day is 16 hours.
∴ x + 0.5y ≤ 16
The profit on a ring is Rs 300 and on a chain is Rs 190. Therefore, profit made from x gold rings and y chains is Rs 300x and Rs 190y respectively.
∴ Total profit, Z = 300x + 190y
Thus, the mathematical formulation of the given problem is:
Maximise Z = 300x + 190y
subject to the constraints
x + y ≤ 24
x + 0.5y ≤ 16
x, y ≥0
First we will convert inequations into equations as follows:
x + y = 24, x + 0.5y = 16, x = 0 and y = 0
Region represented by x + y ≤ 24:
The line x + y = 24 meets the coordinate axes at A(24, 0) and \[B\left( 0, 24 \right)\] respectively. By joining these points we obtain the line x + y = 24. Clearly (0,0) satisfies the x + y = 24. So, the region which contains the origin represents the solution set of the inequation
x + y ≤ 24.
Region represented by x + 0.5y ≤ 16:
The line x + 0.5y = 16 meets the coordinate axes at C(16, 0) and \[D\left( 0, 32 \right)\]
respectively. By joining these points we obtain the line x + 0.5y = 16. Clearly (0,0) satisfies the inequation x + 0.5y ≤ 16. So,the region which contains the origin represents the solution set of the inequation x + 0.5y ≤ 16.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 24, x + 0.5y ≤ 16, x ≥ 0 and y ≥ 0 are as follows.
The feasible region determined by the system
constraints is as follows:
The corner points are O(0, 0), C(16, 0), E(8, 16) and B(0, 24).
The value of Z at these corner points are as follows:
| Corner point |
Z = 300x + 190y |
| O(0, 0) | 0 |
| C(16, 0) | 4800 |
| E(8, 16) | 5440 |
| B(0, 24) | 4560 |
Thus, the maximum value of Z is 5440 at E(8, 16).
Thus, 8 gold rings and 16 chains should be manufactured per day to maximise the profits.
APPEARS IN
संबंधित प्रश्न
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y
Subject to: x + 4y ≤ 24
3x + y ≤ 21
x + y ≤ 9
x ≥ 0, y ≥ 0
Solve the following LPP by graphical method:
Minimize Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Solve the following LPP graphically :
Maximise Z = 105x + 90y
subject to the constraints
x + y ≤ 50
2x + y ≤ 80
x ≥ 0, y ≥ 0.
In order to supplement daily diet, a person wishes to take X and Y tablets. The contents (in milligrams per tablet) of iron, calcium and vitamins in X and Y are given as below :
| Tablets | Iron | Calcium | Vitamin |
| x | 6 | 3 | 2 |
| y | 2 | 3 | 4 |
The person needs to supplement at least 18 milligrams of iron, 21 milligrams of calcium and 16 milligrams of vitamins. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each type should the person take in order to satisfy the above requirement at the minimum cost? Make an LPP and solve graphically.
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = 15x + 10y
Subject to
\[3x + 2y \leq 80\]
\[2x + 3y \leq 70\]
\[ x, y \geq 0\]
Show the solution zone of the following inequalities on a graph paper:
\[5x + y \geq 10\]
\[ x + y \geq 6\]
\[x + 4y \geq 12\]
\[x \geq 0, y \geq 0\]
Find x and y for which 3x + 2y is minimum subject to these inequalities. Use a graphical method.
To maintain one's health, a person must fulfil certain minimum daily requirements for the following three nutrients: calcium, protein and calories. The diet consists of only items I and II whose prices and nutrient contents are shown below:
| Food I | Food II | Minimum daily requirement | |
| Calcium Protein Calories |
10 5 2 |
4 6 6 |
20 20 12 |
| Price | Rs 0.60 per unit | Rs 1.00 per unit |
Find the combination of food items so that the cost may be minimum.
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2 are available. Food F1 costs Rs 4 per unit and F2 costs Rs 6 per unit one unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these foods and also meets the mineral nutritional requirements
A wholesale dealer deals in two kinds, A and B (say) of mixture of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew nuts and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew nuts and 180 grams of hazel nuts. The remainder of both mixtures is per nuts. The dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew nuts and 540 grams of hazel nuts. Mixture A costs Rs 8 per kg. and mixture B costs Rs 12 per kg. Assuming that mixtures A and B are uniform, use graphical method to determine the number of kg. of each mixture which he should use to minimise the cost of the bag.
If a young man drives his vehicle at 25 km/hr, he has to spend Rs 2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to Rs 5/per km. He has Rs 100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
Anil wants to invest at most Rs 12000 in Saving Certificates and National Saving Bonds. According to rules, he has to invest at least Rs 2000 in Saving Certificates and at least Rs 4000 in National Saving Bonds. If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bond is 10% per annum, how much money should he invest to earn maximum yearly income? Find also his maximum yearly income.
A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.
A firm makes items A and B and the total number of items it can make in a day is 24. It takes one hour to make an item of A and half an hour to make an item of B. The maximum time available per day is 16 hours. The profit on an item of A is Rs 300 and on one item of B is Rs 160. How many items of each type should be produced to maximize the profit? Solve the problem graphically.
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at ₹7 profit and that of B at a profit of ₹4. Find the production level per day for maximum profit graphically.
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
By graphical method, the solution of linear programming problem
\[\text{ Subject } to \text{ 3 } x_1 + 2 x_2 \leq 18\]
\[ x_1 \leq 4\]
\[ x_2 \leq 6\]
\[ x_1 \geq 0, x_2 \geq 0, \text{ is } \]
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A
require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours and 20 minutes available for cutting and 4 hours available for assembling. The profit is Rs. 50 each for type A and Rs. 60 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize profit? Formulate the above LPP and solve it graphically and also find the maximum profit.
A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.
Find the graphical solution for the system of linear inequation 2x + y ≤ 2, x − y ≤ 1
The feasible region of an LPP is shown in the figure. If z = 3x + 9y, then the minimum value of z occurs at ______.
The region XOY - plane which is represented by the inequalities -5 ≤ x ≤ 5, -5 ≤ y ≤ 5 is ______
The minimum value of z = 7x + 9y subject to 3x + y ≤ 6, 5x + 8y ≤ 40, x ≥ 0, y ≥ 2 is ______.
In linear programming feasible region (or solution region) for the problem is ____________.
A feasible solution to a linear programming problem
The maximum value of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
Solve the following linear programming problem graphically:
Minimize: Z = 5x + 10y
Subject to constraints:
x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
Solve the following linear programming problem graphically:
Maximize: Z = x + 2y
Subject to constraints:
x + 2y ≥ 100,
2x – y ≤ 0
2x + y ≤ 200,
x ≥ 0, y ≥ 0.
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
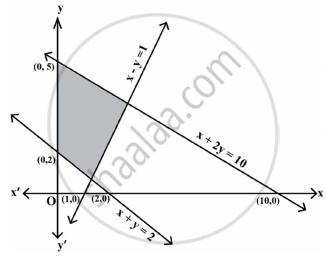
Which of the following is not a constraint to the given Linear Programming Problem?
Solve the following Linear Programming Problem graphically:
Minimize: z = x + 2y,
Subject to the constraints: x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200, x, y ≥ 0.
Minimize z = x + 2y,
Subject to x + 2y ≥ 50, 2x – y ≤ 0, 2x + y ≤ 100, x ≥ 0, y ≥ 0.
Find feasible solution for the following system of linear inequation graphically.
3x + 4y ≥ 12, 4x + 7y ≤ 28, x ≥ 0, y ≥ 0
Aman has ₹ 1500 to purchase rice and wheat for his grocery shop. Each sack of rice and wheat costs ₹ 180 and Rupee ₹ 120 respectively. He can store a maximum number of 10 bags in his shop. He will earn a profit of ₹ 11 per bag of rice and ₹ 9 per bag of wheat.
- Formulate a Linear Programming Problem to maximise Aman’s profit.
- Calculate the maximum profit.
