Advertisements
Advertisements
प्रश्न
Solve the following Linear Programming Problem graphically:
Minimize: z = x + 2y,
Subject to the constraints: x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200, x, y ≥ 0.
उत्तर
The feasible region determined by the constraints, x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200, x, y ≥ 0, is given below.
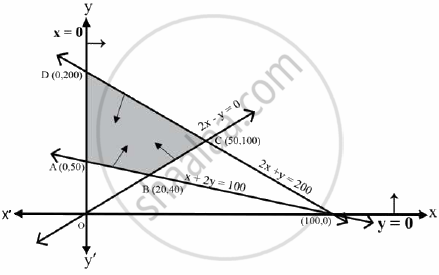
A (0, 50), B (20, 40), C (50, 100) and D (0, 200) are the corner points of the feasible region.
The values of Z at these corner points are given below.
| Corner point | Corresponding value of Z = x + 2y |
|
| A (0, 50) | 100 | Minimum |
| B (20, 40) | 100 | Minimum |
| C (50, 100) | 250 | |
| D (0, 200) | 400 |
The minimum value of Z is 100 at all the points on the line segment joining the points (0, 50) and (20, 40).
APPEARS IN
संबंधित प्रश्न
A dealer in rural area wishes to purchase a number of sewing machines. He has only Rs 5,760 to invest and has space for at most 20 items for storage. An electronic sewing machine cost him Rs 360 and a manually operated sewing machine Rs 240. He can sell an electronic sewing machine at a profit of Rs 22 and a manually operated sewing machine at a profit of Rs 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit? Make it as a LPP and solve it graphically.
Solve the following L.P.P. graphically Maximise Z = 4x + y
Subject to following constraints x + y ≤ 50
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0
A dietician wishes to mix two kinds ·of food X· and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B arid 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin.B | Vitamin C |
| X | 1 unit | 2 unit | 3 unit |
| Y | 2 unit | 2 unit | 1 unit |
Orie kg of food X costs Rs 24 and one kg of food Y costs Rs 36. Using Linear Programming, find the least cost of the total mixture. which will contain the required vitamins.
Solve the following LPP graphically :
Maximise Z = 105x + 90y
subject to the constraints
x + y ≤ 50
2x + y ≤ 80
x ≥ 0, y ≥ 0.
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Maximize Z = 3x + 4y
Subject to
\[2x + 2y \leq 80\]
\[2x + 4y \leq 120\]
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below:
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
Solve the following LPP graphically:
Maximize Z = 20 x + 10 y
Subject to the following constraints
\[x +\]2\[y \leq\]28
3x+ \[y \leq\]24
\[x \geq\] 2x.
\[y \geq\] 0
A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 of calories. Two foods A and B, are available at a cost of Rs 4 and Rs 3 per unit respectively. If one unit of A contains 200 units of vitamin, 1 unit of mineral and 40 calories and one unit of food B contains 100 units of vitamin, 2 units of minerals and 40 calories, find what combination of foods should be used to have the least cost?
A dietician mixes together two kinds of food in such a way that the mixture contains at least 6 units of vitamin A, 7 units of vitamin B, 11 units of vitamin C and 9 units of vitamin D. The vitamin contents of 1 kg of food X and 1 kg of food Y are given below:
| Vitamin A |
Vitamin B |
Vitamin |
Vitamin D |
|
| Food X Food Y |
1 2 |
1 1 |
1 3 |
2 1 |
One kg food X costs Rs 5, whereas one kg of food Y costs Rs 8. Find the least cost of the mixture which will produce the desired diet.
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 11 units of vitamin B. Food P costs ₹60/kg and food Q costs ₹80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
Anil wants to invest at most Rs 12000 in Saving Certificates and National Saving Bonds. According to rules, he has to invest at least Rs 2000 in Saving Certificates and at least Rs 4000 in National Saving Bonds. If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bond is 10% per annum, how much money should he invest to earn maximum yearly income? Find also his maximum yearly income.
A small firm manufacturers items A and B. The total number of items A and B that it can manufacture in a day is at the most 24. Item A takes one hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160, how many of each type of item be produced to maximize the profit? Solve the problem graphically.
A firm makes items A and B and the total number of items it can make in a day is 24. It takes one hour to make an item of A and half an hour to make an item of B. The maximum time available per day is 16 hours. The profit on an item of A is Rs 300 and on one item of B is Rs 160. How many items of each type should be produced to maximize the profit? Solve the problem graphically.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000.
There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
| From \ To | Cost (in ₹) | ||
| A | B | C | |
| P | 160 | 100 | 150 |
| Q | 100 | 120 | 100 |
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Types of Toys | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to product A and product B. Each unit of product A requires 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs. 48 per unit and product B is sold for Rs. 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income? Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
The constraints of an LPP are 7 ≤ x ≤ 12, 8 ≤ y ≤ 13. Determine the vertices of the feasible region formed by them.
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
Maximise and Minimise Z = 3x – 4y subject to x – 2y ≤ 0, – 3x + y ≤ 4, x – y ≤ 6, x, y ≥ 0
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of an L.P.P. is called its ____________.
The maximum value of Z = 3x + 4y subjected to contraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0 and y ≥ 0 is ____________.
A manufacturer wishes to produce two commodities A and B. The number of units of material, labour and equipment needed to produce one unit of each commodity is shown in the table given below. Also shown is the available number of units of each item, material, labour, and equipment.
| Items | Commodity A | Commodity B | Available no. of Units |
| Material | 1 | 2 | 8 |
| Labour | 3 | 2 | 12 |
| Equipment | 1 | 1 | 10 |
Find the maximum profit if each unit of commodity A earns a profit of ₹ 2 and each unit of B earns a profit of ₹ 3.
Any point in the feasible region that gives the optional value (maximum or minimum) of the objective function is called:-
The objective function Z = ax + by of an LPP has maximum vaiue 42 at (4, 6) and minimum value 19 at (3, 2). Which of the following is true?
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
