Advertisements
Advertisements
प्रश्न
Solve the following Linear Programming Problem graphically:
Maximize: z = – x + 2y,
Subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
उत्तर
The feasible region determined by the constraints, x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0 is given below.
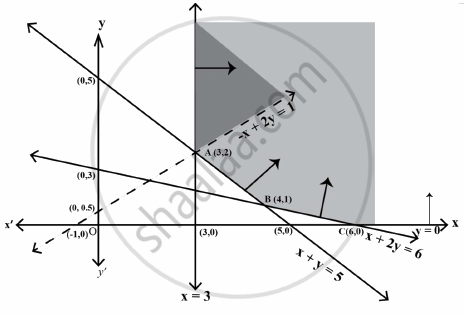
Here, it be seen the can that feasible region is unbounded.
The values of Z at corner points A (3, 2), B (4, 1) and C (6, 0) are given below.
| Corner point | Corresponding value of Z = – x + 2y |
| A (3, 2) | 1 ( may or may not be the maximum value) |
| B (4, 1) | –2 |
| C (6, 0) | –6 |
Since the feasible region is unbounded, Z = 1 may or may not be the maximum value.
Now, we draw the graph of the inequality, – x + 2y > 1, and we check whether the resulting open half-plane has any point/s, in common with the feasible region or not.
Here, the resulting open half plane has points in common with the feasible region.
Hence, Z = 1 is not the maximum value. We conclude, Z has no maximum value.
APPEARS IN
संबंधित प्रश्न
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs 7 profit and B at a profit of Rs 4. Find the production level per day for maximum profit graphically.
A company manufactures bicycles and tricycles each of which must be processed through machines A and B. Machine A has maximum of 120 hours available and machine B has maximum of 180 hours available. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B.
If profits are Rs. 180 for a bicycle and Rs. 220 for a tricycle, formulate and solve the L.P.P. to determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
Maximize Z = 9x + 3y
Subject to
\[2x + 3y \leq 13\]
\[ 3x + y \leq 5\]
\[ x, y \geq 0\]
Maximize Z = 10x + 6y
Subject to
\[3x + y \leq 12\]
\[2x + 5y \leq 34\]
\[ x, y \geq 0\]
Maximize Z = 3x + 4y
Subject to
\[2x + 2y \leq 80\]
\[2x + 4y \leq 120\]
Minimize Z = 30x + 20y
Subject to
\[x + y \leq 8\]
\[ x + 4y \geq 12\]
\[5x + 8y = 20\]
\[ x, y \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Maximize Z = 3x1 + 4x2, if possible,
Subject to the constraints
\[x_1 - x_2 \leq - 1\]
\[ - x_1 + x_2 \leq 0\]
\[ x_1 , x_2 \geq 0\]
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1and F2 are available. Food F1 costs Rs 4 per unit and F2 costs Rs 6 per unit one unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem and find graphically the minimum cost for diet that consists of mixture of these foods and also meets the mineral nutritional requirements
A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum of vitamin A.
A small manufacturer has employed 5 skilled men and 10 semi-skilled men and makes an article in two qualities deluxe model and an ordinary model. The making of a deluxe model requires 2 hrs. work by a skilled man and 2 hrs. work by a semi-skilled man. The ordinary model requires 1 hr by a skilled man and 3 hrs. by a semi-skilled man. By union rules no man may work more than 8 hrs per day. The manufacturers clear profit on deluxe model is Rs 15 and on an ordinary model is Rs 10. How many of each type should be made in order to maximize his total daily profit.
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A company manufactures two articles A and B. There are two departments through which these articles are processed: (i) assembly and (ii) finishing departments. The maximum capacity of the first department is 60 hours a week and that of other department is 48 hours per week. The product of each unit of article A requires 4 hours in assembly and 2 hours in finishing and that of each unit of B requires 2 hours in assembly and 4 hours in finishing. If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B, find the number of units of A and B to be produced per week in order to have maximum profit.
If a young man drives his vehicle at 25 km/hr, he has to spend ₹2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to ₹5 per km. He has ₹100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the number of tennis rackets and cricket bats that the factory must manufacture to earn the maximum profit. Make it as an LPP and solve it graphically.
There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds the she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg, determine how much of each type of fertilizer should be used so that the nutrient requirements are met at minimum cost. What is the minimum cost?
A medical company has factories at two places, A and B. From these places, supply is made to each of its three agencies situated at P, Q and R. The monthly requirements of the agencies are respectively 40, 40 and 50 packets of the medicines, while the production capacity of the factories, A and B, are 60 and 70 packets respectively. The transportation cost per packet from the factories to the agencies are given below:
| Transportation Cost per packet(in Rs.) | ||
| From-> | A | B |
| To | ||
| P | 5 | 4 |
| Q | 4 | 2 |
| R | 3 | 5 |
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to product A and product B. Each unit of product A requires 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs. 48 per unit and product B is sold for Rs. 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income? Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
The region XOY - plane which is represented by the inequalities -5 ≤ x ≤ 5, -5 ≤ y ≤ 5 is ______
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
Of all the points of the feasible region for maximum or minimum of objective function the points.
In Corner point method for solving a linear programming problem the first step is to ____________.
In the Corner point method for solving a linear programming problem the second step after finding the feasible region of the linear programming problem and determining its corner points is ____________.
The maximum value of Z = 3x + 4y subjected to contraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0 and y ≥ 0 is ____________.
The maximum value of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
The objective function Z = x1 + x2, subject to the constraints are x1 + x2 ≤ 10, – 2x1 + 3x2 ≤ 15, x1 ≤ 6, x1, x2 ≥ 0, has maximum value ______ of the feasible region.
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
