Advertisements
Advertisements
प्रश्न
Maximize Z = 3x1 + 4x2, if possible,
Subject to the constraints
\[x_1 - x_2 \leq - 1\]
\[ - x_1 + x_2 \leq 0\]
\[ x_1 , x_2 \geq 0\]
उत्तर
First, we will convert the given inequations into equations, we obtain the following equations:
x1 − x2 = −1, −x1 + x2 = 0, x1 = 0 and x2 = 0
Region represented by x1 − x2 ≤ −1:
The line x1 − x2 = −1 meets the coordinate axes at A(−1, 0) and B(0, 1) respectively. By joining these points we obtain the line x1 − x2 = −1.
Clearly (0,0) does not satisfies the inequation x1 − x2 ≤ −1 .So,the region in the plane which does not contain the origin represents the solution set of the inequation x1 − x2 ≤ −1.
Region represented by −x1 + x2 ≤ 0 or x1 ≥ x2:
The line −x1 + x2 = 0 or x1 = x2 is the line passing through (0, 0).The region to the right of the line x1 = x2 will satisfy the given inequation −x1 + x2 ≤ 0.
If we take a point (1, 3) to the left of the line x1 = x2. Here, 1≤3 which is not satifying the inequation x1 ≥ x2. Therefore, region to the right of the line x1 = x2 will satisfy the given inequation −x1 + x2 ≤ 0.
Region represented by x1 ≥ 0 and x2 ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x1 ≥ 0 and x2 ≥ 0.
The feasible region determined by the system of constraints, x1 − x2 ≤ −1, −x1 + x2 ≤ 0, x1 ≥ 0, and x2 ≥ 0, are as follows.
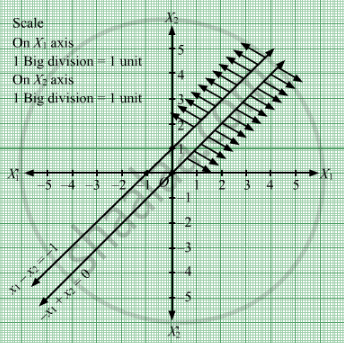
We observe that the feasible region of the given LPP does not exist.
APPEARS IN
संबंधित प्रश्न
Solve the following LPP by using graphical method.
Maximize : Z = 6x + 4y
Subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Also find maximum value of Z.
There are two types of fertilisers 'A' and 'B'. 'A' consists of 12% nitrogen and 5% phosphoric acid whereas 'B' consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If 'A' costs Rs 10 per kg and 'B' cost Rs 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs 7 profit and B at a profit of Rs 4. Find the production level per day for maximum profit graphically.
Find graphically, the maximum value of z = 2x + 5y, subject to constraints given below :
2x + 4y ≤ 83
x + y ≤ 6
x + y ≤ 4
x ≥ 0, y≥ 0
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Solve the following linear programming problem graphically :
Maximise Z = 7x + 10y subject to the constraints
4x + 6y ≤ 240
6x + 3y ≤ 240
x ≥ 10
x ≥ 0, y ≥ 0
Solve the following L.P.P. graphically:
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0 and x, y ≥ 0
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Solve the following LPP graphically:
Maximize Z = 20 x + 10 y
Subject to the following constraints
\[x +\]2\[y \leq\]28
3x+ \[y \leq\]24
\[x \geq\] 2x.
\[y \geq\] 0
Solve the following linear programming problem graphically:
Minimize z = 6 x + 3 y
Subject to the constraints:
4 x + \[y \geq\] 80
x + 5 \[y \geq\] 115
3 x + 2 \[y \leq\] 150
\[x \geq\] 0 , \[y \geq\] 0
A hospital dietician wishes to find the cheapest combination of two foods, A and B, that contains at least 0.5 milligram of thiamin and at least 600 calories. Each unit of Acontains 0.12 milligram of thiamin and 100 calories, while each unit of B contains 0.10 milligram of thiamin and 150 calories. If each food costs 10 paise per unit, how many units of each should be combined at a minimum cost?
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no storage of the other ingredients used in making the cakes.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs ₹16 and one kg of food Y costs ₹20. Find the least cost of the mixture which will produce the required diet?
A manufacturer has three machines installed in his factory. machines I and II are capable of being operated for at most 12 hours whereas Machine III must operate at least for 5 hours a day. He produces only two items, each requiring the use of three machines. The number of hours required for producing one unit each of the items on the three machines is given in the following table:
| Item | Number of hours required by the machine | ||
A B |
I | II | III |
| 1 2 |
2 1 |
1 5/4 |
|
He makes a profit of Rs 6.00 on item A and Rs 4.00 on item B. Assuming that he can sell all that he produces, how many of each item should he produces so as to maximize his profit? Determine his maximum profit. Formulate this LPP mathematically and then solve it.
A manufacturer makes two types A and B of tea-cups. Three machines are needed for the manufacture and the time in minutes required for each cup on the machines is given below:
| Machines | |||
| I | II | III | |
| A B |
12 6 |
18 0 |
6 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each cup A is 75 paise and that on each cup B is 50 paise, show that 15 tea-cups of type A and 30 of type B should be manufactured in a day to get the maximum profit.
A firm manufacturing two types of electric items, A and B, can make a profit of Rs 20 per unit of A and Rs 30 per unit of B. Each unit of A requires 3 motors and 4 transformers and each unit of B requires 2 motors and 4 transformers. The total supply of these per month is restricted to 210 motors and 300 transformers. Type B is an export model requiring a voltage stabilizer which has a supply restricted to 65 units per month. Formulate the linear programing problem for maximum profit and solve it graphically.
A factory uses three different resources for the manufacture of two different products, 20 units of the resources A, 12 units of B and 16 units of C being available. 1 unit of the first product requires 2, 2 and 4 units of the respective resources and 1 unit of the second product requires 4, 2 and 0 units of respective resources. It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Formulate the linear programming problem. How many units of each product should be manufactured for maximizing the profit? Solve it graphically.
A publisher sells a hard cover edition of a text book for Rs 72.00 and paperback edition of the same ext for Rs 40.00. Costs to the publisher are Rs 56.00 and Rs 28.00 per book respectively in addition to weekly costs of Rs 9600.00. Both types require 5 minutes of printing time, although hardcover requires 10 minutes binding time and the paperback requires only 2 minutes. Both the printing and binding operations have 4,800 minutes available each week. How many of each type of book should be produced in order to maximize profit?
A chemical company produces two compounds, A and B. The following table gives the units of ingredients, C and D per kg of compounds A and B as well as minimum requirements of C and D and costs per kg of A and B. Find the quantities of A and B which would give a supply of C and D at a minimum cost.
| Compound | Minimum requirement | ||
| A | B | ||
| Ingredient C Ingredient D |
1 3 |
2 1 |
80 75 |
| Cost (in Rs) per kg | 4 | 6 | - |
A company manufactures two types of novelty Souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours available for assembling. The profit is 50 paise each for type A and 60 paise each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weigh 1 kg and \[1\frac{1}{2}\] kg each respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the books of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically.
A medical company has factories at two places, A and B. From these places, supply is made to each of its three agencies situated at P, Q and R. The monthly requirements of the agencies are respectively 40, 40 and 50 packets of the medicines, while the production capacity of the factories, A and B, are 60 and 70 packets respectively. The transportation cost per packet from the factories to the agencies are given below:
| Transportation Cost per packet(in Rs.) | ||
| From-> | A | B |
| To | ||
| P | 5 | 4 |
| Q | 4 | 2 |
| R | 3 | 5 |
A company manufactures two types of cardigans: type A and type B. It costs ₹ 360 to make a type A cardigan and ₹ 120 to make a type B cardigan. The company can make at most 300 cardigans and spend at most ₹ 72000 a day. The number of cardigans of type B cannot exceed the number of cardigans of type A by more than 200. The company makes a profit of ₹ 100 for each cardigan of type A and ₹ 50 for every cardigan of type B.
Formulate this problem as a linear programming problem to maximize the profit to the company. Solve it graphically and find the maximum profit.
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
For L.P.P. maximize z = 4x1 + 2x2 subject to 3x1 + 2x2 ≥ 9, x1 - x2 ≤ 3, x1 ≥ 0, x2 ≥ 0 has ______.
Area of the region bounded by y = cos x, x = 0, x = π and X-axis is ______ sq.units.
The minimum value of z = 2x + 9y subject to constraints x + y ≥ 1, 2x + 3y ≤ 6, x ≥ 0, y ≥ 0 is ______.
The feasible region of an LPP is shown in the figure. If z = 3x + 9y, then the minimum value of z occurs at ______.
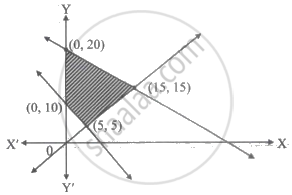
The constraints of an LPP are 7 ≤ x ≤ 12, 8 ≤ y ≤ 13. Determine the vertices of the feasible region formed by them.
The point which provides the solution to the linear programming problem: Max P = 2x + 3y subject to constraints: x ≥ 0, y ≥ 0, 2x + 2y ≤ 9, 2x + y ≤ 7, x + 2y ≤ 8, is ______
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of an L.P.P. is called its ____________.
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then ____________.
Solve the following Linear Programming Problem graphically:
Maximize Z = 400x + 300y subject to x + y ≤ 200, x ≤ 40, x ≥ 20, y ≥ 0
The maximum value of 2x + y subject to 3x + 5y ≤ 26 and 5x + 3y ≤ 30, x ≥ 0, y ≥ 0 is ______.
Solve the following Linear Programming problem graphically:
Maximize: Z = 3x + 3.5y
Subject to constraints:
x + 2y ≥ 240,
3x + 1.5y ≥ 270,
1.5x + 2y ≤ 310,
x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problem graphically.
Maximise Z = 5x + 2y subject to:
x – 2y ≤ 2,
3x + 2y ≤ 12,
– 3x + 2y ≤ 3,
x ≥ 0, y ≥ 0
