Advertisements
Advertisements
Question
Maximize Z = 3x1 + 4x2, if possible,
Subject to the constraints
\[x_1 - x_2 \leq - 1\]
\[ - x_1 + x_2 \leq 0\]
\[ x_1 , x_2 \geq 0\]
Solution
First, we will convert the given inequations into equations, we obtain the following equations:
x1 − x2 = −1, −x1 + x2 = 0, x1 = 0 and x2 = 0
Region represented by x1 − x2 ≤ −1:
The line x1 − x2 = −1 meets the coordinate axes at A(−1, 0) and B(0, 1) respectively. By joining these points we obtain the line x1 − x2 = −1.
Clearly (0,0) does not satisfies the inequation x1 − x2 ≤ −1 .So,the region in the plane which does not contain the origin represents the solution set of the inequation x1 − x2 ≤ −1.
Region represented by −x1 + x2 ≤ 0 or x1 ≥ x2:
The line −x1 + x2 = 0 or x1 = x2 is the line passing through (0, 0).The region to the right of the line x1 = x2 will satisfy the given inequation −x1 + x2 ≤ 0.
If we take a point (1, 3) to the left of the line x1 = x2. Here, 1≤3 which is not satifying the inequation x1 ≥ x2. Therefore, region to the right of the line x1 = x2 will satisfy the given inequation −x1 + x2 ≤ 0.
Region represented by x1 ≥ 0 and x2 ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x1 ≥ 0 and x2 ≥ 0.
The feasible region determined by the system of constraints, x1 − x2 ≤ −1, −x1 + x2 ≤ 0, x1 ≥ 0, and x2 ≥ 0, are as follows.
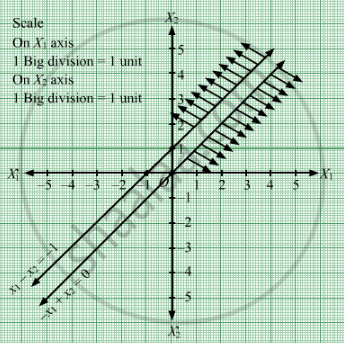
We observe that the feasible region of the given LPP does not exist.
APPEARS IN
RELATED QUESTIONS
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs 7 profit and B at a profit of Rs 4. Find the production level per day for maximum profit graphically.
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Solve the following L.P.P. graphically:
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0 and x, y ≥ 0
Solve the following L.P.P. graphically Maximise Z = 4x + y
Subject to following constraints x + y ≤ 50
3x + y ≤ 90,
x ≥ 10
x, y ≥ 0
Solve the following LPP by graphical method:
Minimize Z = 7x + y subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Maximize Z = 4x + 3y
Subject to
\[3x + 4y \leq 24\]
\[8x + 6y \leq 48\]
\[ x \leq 5\]
\[ y \leq 6\]
\[ x, y \geq 0\]
Maximize Z = −x1 + 2x2
Subject to
\[- x_1 + 3 x_2 \leq 10\]
\[ x_1 + x_2 \leq 6\]
\[ x_1 - x_2 \leq 2\]
\[ x_1 , x_2 \geq 0\]
Show the solution zone of the following inequalities on a graph paper:
\[5x + y \geq 10\]
\[ x + y \geq 6\]
\[x + 4y \geq 12\]
\[x \geq 0, y \geq 0\]
Find x and y for which 3x + 2y is minimum subject to these inequalities. Use a graphical method.
Solve the following linear programming problem graphically:
Minimize z = 6 x + 3 y
Subject to the constraints:
4 x + \[y \geq\] 80
x + 5 \[y \geq\] 115
3 x + 2 \[y \leq\] 150
\[x \geq\] 0 , \[y \geq\] 0
A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum of vitamin A.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs ₹16 and one kg of food Y costs ₹20. Find the least cost of the mixture which will produce the required diet?
If a young man drives his vehicle at 25 km/hr, he has to spend Rs 2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to Rs 5/per km. He has Rs 100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A man owns a field of area 1000 sq.m. He wants to plant fruit trees in it. He has a sum of Rs 1400 to purchase young trees. He has the choice of two types of trees. Type A requires 10 sq.m of ground per tree and costs Rs 20 per tree and type B requires 20 sq.m of ground per tree and costs Rs 25 per tree. When fully grown, type A produces an average of 20 kg of fruit which can be sold at a profit of Rs 2.00 per kg and type B produces an average of 40 kg of fruit which can be sold at a profit of Rs. 1.50 per kg. How many of each type should be planted to achieve maximum profit when the trees are fully grown? What is the maximum profit?
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp while it takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at most 20 hours and the grinding/cutting machine for at most 12 hours. The profit from the sale of a lamp is ₹5.00 and a shade is ₹3.00. Assuming that the manufacturer sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
A small firm manufacturers items A and B. The total number of items A and B that it can manufacture in a day is at the most 24. Item A takes one hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160, how many of each type of item be produced to maximize the profit? Solve the problem graphically.
A company manufactures two articles A and B. There are two departments through which these articles are processed: (i) assembly and (ii) finishing departments. The maximum capacity of the first department is 60 hours a week and that of other department is 48 hours per week. The product of each unit of article A requires 4 hours in assembly and 2 hours in finishing and that of each unit of B requires 2 hours in assembly and 4 hours in finishing. If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B, find the number of units of A and B to be produced per week in order to have maximum profit.
An oil company has two depots, A and B, with capacities of 7000 litres and 4000 litres respectively. The company is to supply oil to three petrol pumps, D, E, F whose requirements are 4500, 3000 and 3500 litres respectively. The distance (in km) between the depots and petrol pumps is given in the following table:
Figure
Assuming that the transportation cost per km is Rs 1.00 per litre, how should the delivery be scheduled in order that the transportation cost is minimum?
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Make an LPP and solve it graphically.
There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds the she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg, determine how much of each type of fertilizer should be used so that the nutrient requirements are met at minimum cost. What is the minimum cost?
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
A farmer has a supply of chemical fertilizer of type A which contains 10% nitrogen and 6% phosphoric acid and of type B which contains 5% nitrogen and 10% phosphoric acid. After the soil test, it is found that at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The fertilizer of type A costs ₹ 5.00 per kg and the type B costs ₹ 8.00 per kg. Using Linear programming, find how many kilograms of each type of fertilizer should be bought to meet the requirement and for the cost to be minimum. Find the feasible region in the graph.
The graph of the inequality 3X − 4Y ≤ 12, X ≤ 1, X ≥ 0, Y ≥ 0 lies in fully in
Sketch the graph of inequation x ≥ 5y in xoy co-ordinate system
Find the feasible solution of linear inequation 2x + 3y ≤ 12, 2x + y ≤ 8, x ≥ 0, y ≥ 0 by graphically
For L.P.P. maximize z = 4x1 + 2x2 subject to 3x1 + 2x2 ≥ 9, x1 - x2 ≤ 3, x1 ≥ 0, x2 ≥ 0 has ______.
Area of the region bounded by y = cos x, x = 0, x = π and X-axis is ______ sq.units.
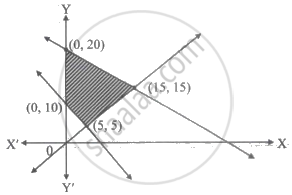
The feasible region of an LPP is shown in the figure. If z = 3x + 9y, then the minimum value of z occurs at ______.
The point which provides the solution to the linear programming problem: Max P = 2x + 3y subject to constraints: x ≥ 0, y ≥ 0, 2x + 2y ≤ 9, 2x + y ≤ 7, x + 2y ≤ 8, is ______
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
The minimum value of z = 7x + 9y subject to 3x + y ≤ 6, 5x + 8y ≤ 40, x ≥ 0, y ≥ 2 is ______.
The feasible region (shaded) for a L.P.P is shown in the figure. The maximum Z = 5x + 7y is ____________.
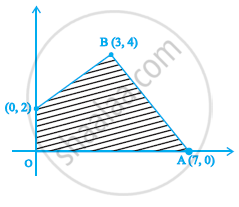
The comer point of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let x = Px + qx where P, q > 0 condition on P and Q so that the maximum of z occurs at both (3, 4) and (0, 5) is
Solve the following Linear Programming Problem graphically:
Minimize: Z = 60x + 80y
Subject to constraints:
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
