Advertisements
Advertisements
Question
A small firm manufacturers items A and B. The total number of items A and B that it can manufacture in a day is at the most 24. Item A takes one hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160, how many of each type of item be produced to maximize the profit? Solve the problem graphically.
Solution
Let the firm manufacture x items of A and y items of B per day.
Number of items cannot be negative.
Therefore, x ≥0 and y ≥0.
It is given that the total number of items manufactured per day is at most 24.
∴ x + y ≤ 24
Item A takes 1 hour to make and item B takes 0.5 hour to make.
The maximum number of hours available per day is 16 hours.
∴ x + 0.5y ≤ 16
If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160.Therefore, profit gained on x items of A and y items of B is
Rs 300x and Rs 160y respectively.
∴ Total profit, Z = 300x + 160y
Thus, the mathematical formulation of the given problem is:
Maximise Z = 300x + 160y
subject to the constraints
x+ y ≤ 24
x + 0.5y ≤ 16
x, y ≥0
First we will convert inequations into equations as follows:
x + y = 24, x + 0.5y = 16, x = 0 and y = 0
Region represented by x + y ≤ 24:
The line x + y = 24 meets the coordinate axes at A1(24, 0) and B1(0, 24) respectively. By joining these points we obtain the line x + y = 24. Clearly (0,0) satisfies the x + y = 24. So, the region which contains the origin represents the solution set of the inequation
x + y ≤ 24.
Region represented by x + 0.5y ≤ 16:
The line x + 0.5y = 16 meets the coordinate axes at C1(16, 0) and D1(0, 32) respectively. By joining these points we obtain the line x + 0.5y = 16. Clearly (0,0) satisfies the inequation x + 0.5y ≤ 16. So,the region which contains the origin represents the solution set of the inequation x + 0.5y ≤ 16.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints x + y ≤ 24, x + 0.5y ≤ 16, x ≥ 0and y ≥ 0 are as follows.
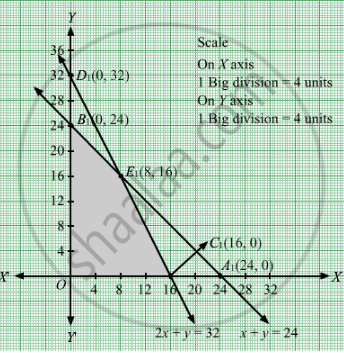
The corner points are O(0, 0) ,C1(16, 0), E1(8, 16) and B1(0, 24).
The value of Z at these corner points are as follows:
| Corner point | Z = 300x + 160y |
| O(0, 0) | 0 |
| C1(16, 0) | 4800 |
| E1(8, 16) | 4960 |
| B1(0, 24) | 3840 |
Thus, the maximum value of Z is 4960 at E1(8, 16).
Thus, 8 units of item A and 16 units of item B should be manufactured per day to maximise the profits.
APPEARS IN
RELATED QUESTIONS
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
A company manufactures bicycles and tricycles each of which must be processed through machines A and B. Machine A has maximum of 120 hours available and machine B has maximum of 180 hours available. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B.
If profits are Rs. 180 for a bicycle and Rs. 220 for a tricycle, formulate and solve the L.P.P. to determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
A dietician wishes to mix two kinds ·of food X· and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B arid 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin.B | Vitamin C |
| X | 1 unit | 2 unit | 3 unit |
| Y | 2 unit | 2 unit | 1 unit |
Orie kg of food X costs Rs 24 and one kg of food Y costs Rs 36. Using Linear Programming, find the least cost of the total mixture. which will contain the required vitamins.
Solve the following LPP graphically :
Maximise Z = 105x + 90y
subject to the constraints
x + y ≤ 50
2x + y ≤ 80
x ≥ 0, y ≥ 0.
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 10x + 6y
Subject to
\[3x + y \leq 12\]
\[2x + 5y \leq 34\]
\[ x, y \geq 0\]
Minimize Z = 5x + 3y
Subject to
\[2x + y \geq 10\]
\[x + 3y \geq 15\]
\[ x \leq 10\]
\[ y \leq 8\]
\[ x, y \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Maximize Z = 3x1 + 4x2, if possible,
Subject to the constraints
\[x_1 - x_2 \leq - 1\]
\[ - x_1 + x_2 \leq 0\]
\[ x_1 , x_2 \geq 0\]
Show the solution zone of the following inequalities on a graph paper:
\[5x + y \geq 10\]
\[ x + y \geq 6\]
\[x + 4y \geq 12\]
\[x \geq 0, y \geq 0\]
Find x and y for which 3x + 2y is minimum subject to these inequalities. Use a graphical method.
A diet of two foods F1 and F2 contains nutrients thiamine, phosphorous and iron. The amount of each nutrient in each of the food (in milligrams per 25 gms) is given in the following table:
Nutrients |
Food |
F1 | F2 |
| Thiamine | 0.25 | 0.10 |
|
| Phosphorous | 0.75 | 1.50 | |
| Iron | 1.60 | 0.80 | |
The minimum requirement of the nutrients in the diet are 1.00 mg of thiamine, 7.50 mg of phosphorous and 10.00 mg of iron. The cost of F1 is 20 paise per 25 gms while the cost of F2 is 15 paise per 25 gms. Find the minimum cost of diet.
To maintain one's health, a person must fulfil certain minimum daily requirements for the following three nutrients: calcium, protein and calories. The diet consists of only items I and II whose prices and nutrient contents are shown below:
| Food I | Food II | Minimum daily requirement | |
| Calcium Protein Calories |
10 5 2 |
4 6 6 |
20 20 12 |
| Price | Rs 0.60 per unit | Rs 1.00 per unit |
Find the combination of food items so that the cost may be minimum.
A wholesale dealer deals in two kinds, A and B (say) of mixture of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew nuts and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew nuts and 180 grams of hazel nuts. The remainder of both mixtures is per nuts. The dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew nuts and 540 grams of hazel nuts. Mixture A costs Rs 8 per kg. and mixture B costs Rs 12 per kg. Assuming that mixtures A and B are uniform, use graphical method to determine the number of kg. of each mixture which he should use to minimise the cost of the bag.
Two tailors, A and B earn Rs 15 and Rs 20 per day respectively. A can stitch 6 shirts and 4 pants while B can stitch 10 shirts and 4 pants per day. How many days shall each work if it is desired to produce (at least) 60 shirts and 32 pants at a minimum labour cost?
A factory uses three different resources for the manufacture of two different products, 20 units of the resources A, 12 units of B and 16 units of C being available. 1 unit of the first product requires 2, 2 and 4 units of the respective resources and 1 unit of the second product requires 4, 2 and 0 units of respective resources. It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Formulate the linear programming problem. How many units of each product should be manufactured for maximizing the profit? Solve it graphically.
Anil wants to invest at most Rs 12000 in Saving Certificates and National Saving Bonds. According to rules, he has to invest at least Rs 2000 in Saving Certificates and at least Rs 4000 in National Saving Bonds. If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bond is 10% per annum, how much money should he invest to earn maximum yearly income? Find also his maximum yearly income.
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp while it takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at most 20 hours and the grinding/cutting machine for at most 12 hours. The profit from the sale of a lamp is ₹5.00 and a shade is ₹3.00. Assuming that the manufacturer sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A box manufacturer makes large and small boxes from a large piece of cardboard. The large boxes require 4 sq. metre per box while the small boxes require 3 sq. metre per box. The manufacturer is required to make at least three large boxes and at least twice as many small boxes as large boxes. If 60 sq. metre of cardboard is in stock, and if the profits on the large and small boxes are Rs 3 and Rs 2 per box, how many of each should be made in order to maximize the total profit?
A manufacturer makes two products, A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 units of product A and 16 units of product B. A working week consists of 40 hours of production and the weekly turn over must not be less than Rs 10000. If the profit on each of product A is Rs 20 and an product B is Rs 30, then how many of each should be produced so that the profit is maximum? Also find the maximum profit.
If a young man drives his vehicle at 25 km/hr, he has to spend ₹2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to ₹5 per km. He has ₹100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
| From \ To | Cost (in ₹) | ||
| A | B | C | |
| P | 160 | 100 | 150 |
| Q | 100 | 120 | 100 |
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
A manufacturer considers that men and women workers are equally efficient and so he pays them at the same rate. He has 30 and 17 units of workers (male and female) and capital respectively, which he uses to produce two types of goods A and B. To produce one unit of A, 2 workers and 3 units of capital are required while 3 workers and 1 unit of capital is required to produce one unit of B. If A and B are priced at ₹100 and ₹120 per unit respectively, how should he use his resources to maximise the total revenue? Form the above as an LPP and solve graphically. Do you agree with this view of the manufacturer that men and women workers are equally efficient and so should be paid at the same rate?
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
The minimum value of z = 2x + 9y subject to constraints x + y ≥ 1, 2x + 3y ≤ 6, x ≥ 0, y ≥ 0 is ______.
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of an L.P.P. is called its ____________.
Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at ____________.
In linear programming feasible region (or solution region) for the problem is ____________.
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then ____________.
In Corner point method for solving a linear programming problem the first step is to ____________.
Minimise z = – 3x + 4y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0 What will be the minimum value of z ?
The maximum value of 2x + y subject to 3x + 5y ≤ 26 and 5x + 3y ≤ 30, x ≥ 0, y ≥ 0 is ______.
Solve the following Linear Programming Problem graphically.
Maximise Z = 5x + 2y subject to:
x – 2y ≤ 2,
3x + 2y ≤ 12,
– 3x + 2y ≤ 3,
x ≥ 0, y ≥ 0
If x – y ≥ 8, x ≥ 3, y ≥ 3, x ≥ 0, y ≥ 0 then find the coordinates of the corner points of the feasible region.
Aman has ₹ 1500 to purchase rice and wheat for his grocery shop. Each sack of rice and wheat costs ₹ 180 and Rupee ₹ 120 respectively. He can store a maximum number of 10 bags in his shop. He will earn a profit of ₹ 11 per bag of rice and ₹ 9 per bag of wheat.
- Formulate a Linear Programming Problem to maximise Aman’s profit.
- Calculate the maximum profit.
