Advertisements
Advertisements
Question
Maximize Z = 10x + 6y
Subject to
\[3x + y \leq 12\]
\[2x + 5y \leq 34\]
\[ x, y \geq 0\]
Advertisements
Solution
First, we will convert the given inequations into equations, we obtain the following equations:
3x + y = 12, 2x + 5y = 34, x = 0 and y = 0
Region represented by 3x + y ≤ 12:
The line 3x + y = 12 meets the coordinate axes at \[A\left( 4, 0 \right)\] and \[B\left( 0, 12 \right)\] respectively. By joining these points we obtain the line 3x + y = 12.
Clearly (0,0) satisfies the inequation 3x + y ≤ 12. So,the region containing the origin represents the solution set of the inequation 3x + y ≤ 12 .
Region represented by 2x + 5y ≤ 34:
The line 2x + 5y = 34 meets the coordinate axes at \[C\left( 17, 0 \right)\] and \[D\left( 0, \frac{34}{5} \right)\]
respectively. By joining these points we obtain the line 2x + 5y ≤ 34.
Clearly (0,0) satisfies the inequation 2x + 5y ≤ 34. So,the region containing the origin represents the solution set of the inequation 2x + 5y ≤ 34.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints, 3x + y ≤ 12, 2x + 5y ≤ 34, x ≥ 0, and y ≥ 0 are as follows.
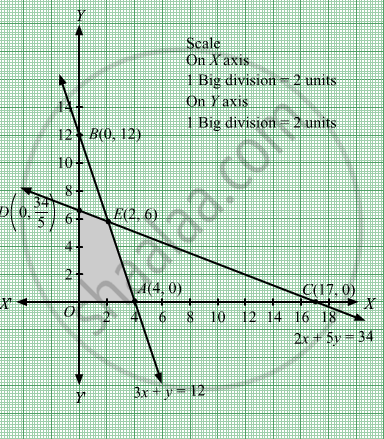
The corner points of the feasible region are O(0, 0), \[A\left( 4, 0 \right)\], \[E\left( 2, 6 \right)\] and \[D\left( 0, \frac{34}{5} \right)\] .
The values of Z at these corner points are as follows:
| Corner point | Z = 10x + 6y |
| O(0, 0) | 10 × 0 + 6 × 0 = 0 |
|
\[A\left( 4, 0 \right)\]
|
10× 4 + 6 × 0 = 40 |
|
\[E\left( 2, 6 \right)\]
|
10 × 2 + 6 × 6 = 56 |
|
\[D\left( 0, \frac{34}{5} \right)\]
|
10 × 0 + 6 × \[\frac{34}{5}\] = \[\frac{204}{3}\]
|
We see that the maximum value of the objective function Z is 56 which is at \[E\left( 2, 6 \right)\] that means at x = 2 and y = 6.
Thus, the optimal value of Z is 56.
APPEARS IN
RELATED QUESTIONS
A company manufactures bicycles and tricycles each of which must be processed through machines A and B. Machine A has maximum of 120 hours available and machine B has maximum of 180 hours available. Manufacturing a bicycle requires 6 hours on machine A and 3 hours on machine B. Manufacturing a tricycle requires 4 hours on machine A and 10 hours on machine B.
If profits are Rs. 180 for a bicycle and Rs. 220 for a tricycle, formulate and solve the L.P.P. to determine the number of bicycles and tricycles that should be manufactured in order to maximize the profit.
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Minimize Z = 2x + 4y
Subject to
\[x + y \geq 8\]
\[x + 4y \geq 12\]
\[x \geq 3, y \geq 2\]
Minimize Z = 5x + 3y
Subject to
\[2x + y \geq 10\]
\[x + 3y \geq 15\]
\[ x \leq 10\]
\[ y \leq 8\]
\[ x, y \geq 0\]
Minimize Z = x − 5y + 20
Subject to
\[x - y \geq 0\]
\[ - x + 2y \geq 2\]
\[ x \geq 3\]
\[ y \leq 4\]
\[ x, y \geq 0\]
Maximize Z = 3x + 3y, if possible,
Subject to the constraints
\[x - y \leq 1\]
\[x + y \geq 3\]
\[ x, y \geq 0\]
A diet for a sick person must contain at least 4000 units of vitamins, 50 units of minerals and 1400 of calories. Two foods A and B, are available at a cost of Rs 4 and Rs 3 per unit respectively. If one unit of A contains 200 units of vitamin, 1 unit of mineral and 40 calories and one unit of food B contains 100 units of vitamin, 2 units of minerals and 40 calories, find what combination of foods should be used to have the least cost?
To maintain one's health, a person must fulfil certain minimum daily requirements for the following three nutrients: calcium, protein and calories. The diet consists of only items I and II whose prices and nutrient contents are shown below:
| Food I | Food II | Minimum daily requirement | |
| Calcium Protein Calories |
10 5 2 |
4 6 6 |
20 20 12 |
| Price | Rs 0.60 per unit | Rs 1.00 per unit |
Find the combination of food items so that the cost may be minimum.
A manufacturer makes two types A and B of tea-cups. Three machines are needed for the manufacture and the time in minutes required for each cup on the machines is given below:
| Machines | |||
| I | II | III | |
| A B |
12 6 |
18 0 |
6 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each cup A is 75 paise and that on each cup B is 50 paise, show that 15 tea-cups of type A and 30 of type B should be manufactured in a day to get the maximum profit.
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?
A furniture manufacturing company plans to make two products : chairs and tables. From its available resources which consists of 400 square feet to teak wood and 450 man hours. It is known that to make a chair requires 5 square feet of wood and 10 man-hours and yields a profit of Rs 45, while each table uses 20 square feet of wood and 25 man-hours and yields a profit of Rs 80. How many items of each product should be produced by the company so that the profit is maximum?
A firm manufactures two products A and B. Each product is processed on two machines M1 and M2. Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2. The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs 3 and Rs 4 respectively.
Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs 50 each on type A and Rs 60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
A box manufacturer makes large and small boxes from a large piece of cardboard. The large boxes require 4 sq. metre per box while the small boxes require 3 sq. metre per box. The manufacturer is required to make at least three large boxes and at least twice as many small boxes as large boxes. If 60 sq. metre of cardboard is in stock, and if the profits on the large and small boxes are Rs 3 and Rs 2 per box, how many of each should be made in order to maximize the total profit?
A library has to accommodate two different types of books on a shelf. The books are 6 cm and 4 cm thick and weigh 1 kg and \[1\frac{1}{2}\] kg each respectively. The shelf is 96 cm long and atmost can support a weight of 21 kg. How should the shelf be filled with the books of two types in order to include the greatest number of books? Make it as an LPP and solve it graphically.
A cooperative society of farmers has 50 hectares of land to grow two crops X and Y. The profits from crops X and Y per hectare are estimated as ₹10,500 and ₹9,000 respectively. To control weeds, a liquid herbicide has to be used for crops X and Y at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. How much land should be allocated to each crop so as to maximise the total profit of the society?
A manufacturing company makes two models A and B of a product. Each piece of model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of ₹8000 on each piece of model A and ₹12000 on each piece of model B. How many pieces of model A and model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?
A manufacturer has three machine I, II, III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine III must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines.
The number of hours required for producing 1 unit each of M and N on the three machines are given in the following table:
| Items | Number of hours required on machines | ||
| I | II | III | |
| M | 1 | 2 | 1 |
| N | 2 | 1 | 1.25 |
She makes a profit of ₹600 and ₹400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below:
| From \ To | Cost (in ₹) | ||
| A | B | C | |
| P | 160 | 100 | 150 |
| Q | 100 | 120 | 100 |
How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
Find the graphical solution for the system of linear inequation 2x + y ≤ 2, x − y ≤ 1
For L.P.P. maximize z = 4x1 + 2x2 subject to 3x1 + 2x2 ≥ 9, x1 - x2 ≤ 3, x1 ≥ 0, x2 ≥ 0 has ______.
The minimum value of z = 2x + 9y subject to constraints x + y ≥ 1, 2x + 3y ≤ 6, x ≥ 0, y ≥ 0 is ______.
The feasible region of an LPP is shown in the figure. If z = 3x + 9y, then the minimum value of z occurs at ______.
The maximum value of z = 3x + 10y subjected to the conditions 5x + 2y ≤ 10, 3x + 5y ≤ 15, x, y ≥ 0 is ______.
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
The minimum value of z = 7x + 9y subject to 3x + y ≤ 6, 5x + 8y ≤ 40, x ≥ 0, y ≥ 2 is ______.
Maximise and Minimise Z = 3x – 4y subject to x – 2y ≤ 0, – 3x + y ≤ 4, x – y ≤ 6, x, y ≥ 0
Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at ____________.
In linear programming feasible region (or solution region) for the problem is ____________.
Solve the following Linear Programming Problem graphically:
Maximize Z = 400x + 300y subject to x + y ≤ 200, x ≤ 40, x ≥ 20, y ≥ 0
The constraints –x1 + x2 ≤ 1, –x1 + 3x2 ≤ 9, x1x2 ≥ 0 define on ______.
The maximum value of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
The shaded part of given figure indicates in feasible region, then the constraints are:
Solve the following Linear Programming Problem graphically:
Maximize: z = – x + 2y,
Subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Aman has ₹ 1500 to purchase rice and wheat for his grocery shop. Each sack of rice and wheat costs ₹ 180 and Rupee ₹ 120 respectively. He can store a maximum number of 10 bags in his shop. He will earn a profit of ₹ 11 per bag of rice and ₹ 9 per bag of wheat.
- Formulate a Linear Programming Problem to maximise Aman’s profit.
- Calculate the maximum profit.
