Advertisements
Advertisements
Question
Maximize Z = 7x + 10y
Subject to
\[x + y \leq 30000\]
\[ y \leq 12000\]
\[ x \geq 6000\]
\[ x \geq y\]
\[ x, y \geq 0\]
Solution
We have to maximize Z = 7x + 10y
First, we will convert the given inequations into equations, we obtain the following equations:
x + y = 30000,y = 12000, x = 6000, x = y, x = 0 and y = 0.
Region represented by x + y ≤ 30000:
The line x + y = 30000 meets the coordinate axes at \[A\left( 30000, 0 \right)\] and \[B\left( 0, 30000 \right)\] respectively. By joining these points we obtain the line x + y = 30000.
Clearly (0,0) satisfies the inequation x + y ≤ 30000. So,the region containing the origin represents the solution set of the inequation x + y ≤ 30000.
The line y = 12000 is the line that passes through C(0,12000) and parallel to x axis.
The line x = 6000 is the line that passes through (6000, 0) and parallel to y axis.
Region represented by x ≥ y
The line x = y is the line that passes through origin.The points to the right of the line x= y satisfy the inequation x ≥ y.
Like by taking the point (−12000, 6000).Here, 6000 > −12000 which implies y > x. Hence, the points to the left of the line x = y will not satisfy the given inequation x ≥ y.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0 and y ≥ 0.
The feasible region determined by the system of constraints, x + y ≤ 30000, y ≤ 12000, x ≥ 6000, x ≥ y , x ≥ 0 and y ≥ 0 are as follows:
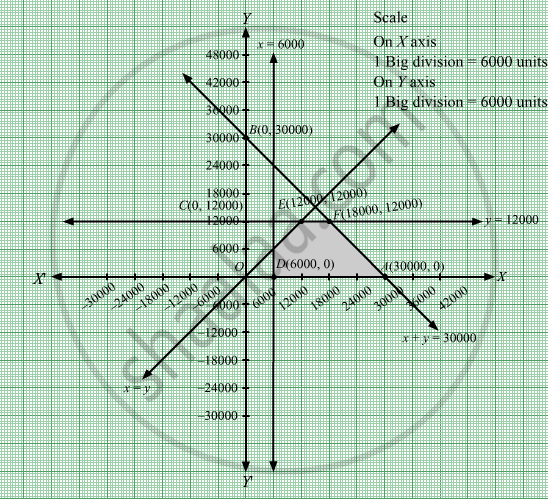
The corner points of the feasible region are D(6000, 0), \[A\left( 3000, 0 \right)\] , \[F\left( 18000, 12000 \right)\] and \[E\left( 12000, 12000 \right)\] .
The values of Z at these corner points are as follows:
| Corner point | Z = 7x + 10y |
| D(6000, 0) | 7 × 6000 + 10 × 0 = 42000 |
|
\[A\left( 3000, 0 \right)\]
|
7× 3000 + 10 × 0 = 21000 |
|
\[F\left( 18000, 12000 \right)\]
|
7 × 18000 + 10 × 12000 = 246000 |
|
\[E\left( 12000, 12000 \right)\]
|
7 × 12000 + 10 ×12000 = 204000 |
We see that the maximum value of the objective function Z is 246000 which is at \[F\left( 18000, 12000 \right)\] that means at x = 18000 and y = 12000.
Thus, the optimal value of Z is 246000.
APPEARS IN
RELATED QUESTIONS
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
Minimize :Z=6x+4y
Subject to : 3x+2y ≥12
x+y ≥5
0 ≤x ≤4
0 ≤ y ≤ 4
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs 7 profit and B at a profit of Rs 4. Find the production level per day for maximum profit graphically.
Solve the following L.P.P graphically: Maximise Z = 20x + 10y
Subject to the following constraints x + 2y ≤ 28,
3x + y ≤ 24,
x ≥ 2,
x, y ≥ 0
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Minimize Z = 2x + 4y
Subject to
\[x + y \geq 8\]
\[x + 4y \geq 12\]
\[x \geq 3, y \geq 2\]
Minimize Z = 30x + 20y
Subject to
\[x + y \leq 8\]
\[ x + 4y \geq 12\]
\[5x + 8y = 20\]
\[ x, y \geq 0\]
Maximize Z = −x1 + 2x2
Subject to
\[- x_1 + 3 x_2 \leq 10\]
\[ x_1 + x_2 \leq 6\]
\[ x_1 - x_2 \leq 2\]
\[ x_1 , x_2 \geq 0\]
Maximize Z = 3x + 3y, if possible,
Subject to the constraints
\[x - y \leq 1\]
\[x + y \geq 3\]
\[ x, y \geq 0\]
Solved the following linear programming problem graphically:
Maximize Z = 60x + 15y
Subject to constraints
\[x + y \leq 50\]
\[3x + y \leq 90\]
\[ x, y \geq 0\]
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 11 units of vitamin B. Food P costs ₹60/kg and food Q costs ₹80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
One kind of cake requires 200 g of flour and 25 g of fat, and another kind of cake requires 100 g of flour and 50 g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no storage of the other ingredients used in making the cakes.
A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires atleast 240 units of calcium, atleast 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum of vitamin A.
A manufacturer of Furniture makes two products : chairs and tables. processing of these products is done on two machines A and B. A chair requires 2 hrs on machine A and 6 hrs on machine B. A table requires 4 hrs on machine A and 2 hrs on machine B. There are 16 hrs of time per day available on machine A and 30 hrs on machine B. Profit gained by the manufacturer from a chair and a table is Rs 3 and Rs 5 respectively. Find with the help of graph what should be the daily production of each of the two products so as to maximize his profit.
A chemical company produces two compounds, A and B. The following table gives the units of ingredients, C and D per kg of compounds A and B as well as minimum requirements of C and D and costs per kg of A and B. Find the quantities of A and B which would give a supply of C and D at a minimum cost.
| Compound | Minimum requirement | ||
| A | B | ||
| Ingredient C Ingredient D |
1 3 |
2 1 |
80 75 |
| Cost (in Rs) per kg | 4 | 6 | - |
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats of first class. However, at least 4 times as many passengers prefer to travel by economy class to the first class. Determine how many each type of tickets must be sold in order to maximize the profit for the airline. What is the maximum profit.
A manufacturer makes two products, A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 units of product A and 16 units of product B. A working week consists of 40 hours of production and the weekly turn over must not be less than Rs 10000. If the profit on each of product A is Rs 20 and an product B is Rs 30, then how many of each should be produced so that the profit is maximum? Also find the maximum profit.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Make an LPP and solve it graphically.
A cooperative society of farmers has 50 hectares of land to grow two crops X and Y. The profits from crops X and Y per hectare are estimated as ₹10,500 and ₹9,000 respectively. To control weeds, a liquid herbicide has to be used for crops X and Y at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. How much land should be allocated to each crop so as to maximise the total profit of the society?
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time.
(i) What number of rackets and bats must be made if the factory is to work at full capacity?
(ii) If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000.
Tow godowns, A and B, have grain storage capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F, whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:
| Transportation cost per quintal(in Rs.) | ||
| From-> | A | B |
| To | ||
| D | 6.00 | 4.00 |
| E | 3.00 | 2.00 |
| F | 2.50 | 3.00 |
How should the supplies be transported in order that the transportation cost is minimum?
Maximize: z = 3x + 5y Subject to
x +4y ≤ 24 3x + y ≤ 21
x + y ≤ 9 x ≥ 0 , y ≥0
The maximum value of z = 6x + 8y subject to x - y ≥ 0, x + 3y ≤ 12, x ≥ 0, y ≥ 0 is ______.
For L.P.P. maximize z = 4x1 + 2x2 subject to 3x1 + 2x2 ≥ 9, x1 - x2 ≤ 3, x1 ≥ 0, x2 ≥ 0 has ______.
The maximum value of Z = 5x + 4y, Subject to y ≤ 2x, x ≤ 2y, x + y ≤ 3, x ≥ 0, y ≥ 0 is ______.
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is ______.
Z = 20x1 + 20x2, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at ____________.
In linear programming feasible region (or solution region) for the problem is ____________.
In the Corner point method for solving a linear programming problem the second step after finding the feasible region of the linear programming problem and determining its corner points is ____________.
A feasible solution to a linear programming problem
A manufacturer wishes to produce two commodities A and B. The number of units of material, labour and equipment needed to produce one unit of each commodity is shown in the table given below. Also shown is the available number of units of each item, material, labour, and equipment.
| Items | Commodity A | Commodity B | Available no. of Units |
| Material | 1 | 2 | 8 |
| Labour | 3 | 2 | 12 |
| Equipment | 1 | 1 | 10 |
Find the maximum profit if each unit of commodity A earns a profit of ₹ 2 and each unit of B earns a profit of ₹ 3.
The solution set of the inequality 3x + 5y < 4 is ______.
The shaded part of given figure indicates in feasible region, then the constraints are:

Solve the following linear programming problem graphically:
Maximize: Z = x + 2y
Subject to constraints:
x + 2y ≥ 100,
2x – y ≤ 0
2x + y ≤ 200,
x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problem graphically:
Minimize: Z = 60x + 80y
Subject to constraints:
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
Solve the following Linear Programming Problem graphically.
Maximise Z = 5x + 2y subject to:
x – 2y ≤ 2,
3x + 2y ≤ 12,
– 3x + 2y ≤ 3,
x ≥ 0, y ≥ 0
If x – y ≥ 8, x ≥ 3, y ≥ 3, x ≥ 0, y ≥ 0 then find the coordinates of the corner points of the feasible region.
