Advertisements
Advertisements
Question
A manufacturer makes two products, A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 units of product A and 16 units of product B. A working week consists of 40 hours of production and the weekly turn over must not be less than Rs 10000. If the profit on each of product A is Rs 20 and an product B is Rs 30, then how many of each should be produced so that the profit is maximum? Also find the maximum profit.
Solution
Let x units of product A and y units of product B were manufactured.
Number of units cannot be negative.
Therefore, \[x, y \geq 0\]
According to question, the given information can be tabulated as:
| Selling price(Rs) | Manufacturing time(hrs) | |
| Product A(x) | 200 | 0.5 |
| Product B(y) | 300 | 1 |
Also, the availability of time is 40 hours and the revenue should be atleast Rs 10000.
Further, it is given that there is a permanent order for 14 units of product A and 16 units of product B.
Therefore, the constraints are
\[200x + 300y \geq 10000\]
\[0 . 5x + y \leq 40\]
\[x \geq 14\]
\[y \geq 16\]
If the profit on each of product A is Rs 20 and on product B is Rs 30.Therefore, profit gained on x units of product A and y units of product B is Rs 20x and Rs 30y respectively.
Total profit = Z = \[20x + 30y\] which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = \[20x + 30y\]
subject to
\[2x + 3y \geq 100\]
\[x + 2y \leq 80\]
\[x \geq 14\]
\[y \geq 16\]
First we will convert inequations into equations as follows:
2x + 3y = 100, x + 2y = 80, x = 14, y = 16, x = 0 and y = 0.
Region represented by 2x + 3y ≥ 100:
The line 2x + 3y = 100 meets the coordinate axes at A1(50, 0) and \[B_1 \left( 0, \frac{100}{3} \right)\] respectively. By joining these points we obtain the line
2x + 3y = 100 . Clearly (0,0) does not satisfies the 2x + 3y = 100. So, the region which does not contain the origin represents the solution set of the inequation 2x + 3y ≥ 100.
Region represented by x + 2y ≤ 80:
The line x + 2y = 80 meets the coordinate axes at C1(80, 0) and D1(0, 40) respectively. By joining these points we obtain the line
x + 2y = 80. Clearly (0,0) satisfies the inequation x + 2y ≤ 80. So,the region which contains the origin represents the solution set of the inequation x + 2y ≤ 80.
Region represented by x ≥ 14
x = 14 is the line passes through (14, 0) and is parallel to the Y axis.The region to the right of the line x = 14 will satisfy the inequation.
Region represented by y ≥ 16
y = 16 is the line passes through (0, 16) and is parallel to the X axis.The region above the line y = 16 will satisfy the inequation.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 3y ≥ 100, x + 2y ≤ 80, x≥ 14, y ≥ 16, x ≥ 0 and y ≥ 0 are as follows.
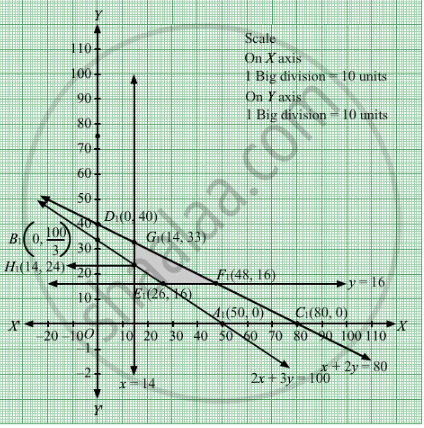The corner points of the feasible region are E1(26, 16), F1(48, 16), G1(14, 33) and H1(14, 24)
The values of Z at these corner points are as follows
| Corner point | Z= 20x + 30y |
| E1 | 1000 |
| F1 | 1440 |
| G1 | 1270 |
| H1 | 1000 |
The maximum value of Z is Rs 1440 which is attained at F1
APPEARS IN
RELATED QUESTIONS
A retired person wants to invest an amount of Rs. 50, 000. His broker recommends investing in two type of bonds ‘A’ and ‘B’ yielding 10% and 9% return respectively on the invested amount. He decides to invest at least Rs. 20,000 in bond ‘A’ and at least Rs. 10,000 in bond ‘B’. He also wants to invest at least as much in bond ‘A’ as in bond ‘B’. Solve this linear programming problem graphically to maximise his returns.
Minimum and maximum z = 5x + 2y subject to the following constraints:
x-2y ≤ 2
3x+2y ≤ 12
-3x+2y ≤ 3
x ≥ 0,y ≥ 0
Solve the following L.P.P graphically: Maximise Z = 20x + 10y
Subject to the following constraints x + 2y ≤ 28,
3x + y ≤ 24,
x ≥ 2,
x, y ≥ 0
A dietician wishes to mix two kinds ·of food X· and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B arid 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin.B | Vitamin C |
| X | 1 unit | 2 unit | 3 unit |
| Y | 2 unit | 2 unit | 1 unit |
Orie kg of food X costs Rs 24 and one kg of food Y costs Rs 36. Using Linear Programming, find the least cost of the total mixture. which will contain the required vitamins.
Solve the following LPP graphically :
Maximise Z = 105x + 90y
subject to the constraints
x + y ≤ 50
2x + y ≤ 80
x ≥ 0, y ≥ 0.
Maximize Z = 5x + 3y
Subject to
\[3x + 5y \leq 15\]
\[5x + 2y \leq 10\]
\[ x, y \geq 0\]
Maximize Z = 9x + 3y
Subject to
\[2x + 3y \leq 13\]
\[ 3x + y \leq 5\]
\[ x, y \geq 0\]
Maximize Z = 50x + 30y
Subject to
\[2x + y \leq 18\]
\[3x + 2y \leq 34\]
\[ x, y \geq 0\]
Minimize Z = 5x + 3y
Subject to
\[2x + y \geq 10\]
\[x + 3y \geq 15\]
\[ x \leq 10\]
\[ y \leq 8\]
\[ x, y \geq 0\]
Minimize Z = x − 5y + 20
Subject to
\[x - y \geq 0\]
\[ - x + 2y \geq 2\]
\[ x \geq 3\]
\[ y \leq 4\]
\[ x, y \geq 0\]
Minimize Z = 3x1 + 5x2
Subject to
\[x_1 + 3 x_2 \geq 3\]
\[ x_1 + x_2 \geq 2\]
\[ x_1 , x_2 \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Find graphically, the maximum value of Z = 2x + 5y, subject to constraints given below:
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
A diet of two foods F1 and F2 contains nutrients thiamine, phosphorous and iron. The amount of each nutrient in each of the food (in milligrams per 25 gms) is given in the following table:
Nutrients |
Food |
F1 | F2 |
| Thiamine | 0.25 | 0.10 |
|
| Phosphorous | 0.75 | 1.50 | |
| Iron | 1.60 | 0.80 | |
The minimum requirement of the nutrients in the diet are 1.00 mg of thiamine, 7.50 mg of phosphorous and 10.00 mg of iron. The cost of F1 is 20 paise per 25 gms while the cost of F2 is 15 paise per 25 gms. Find the minimum cost of diet.
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 11 units of vitamin B. Food P costs ₹60/kg and food Q costs ₹80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs ₹16 and one kg of food Y costs ₹20. Find the least cost of the mixture which will produce the required diet?
A factory uses three different resources for the manufacture of two different products, 20 units of the resources A, 12 units of B and 16 units of C being available. 1 unit of the first product requires 2, 2 and 4 units of the respective resources and 1 unit of the second product requires 4, 2 and 0 units of respective resources. It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Formulate the linear programming problem. How many units of each product should be manufactured for maximizing the profit? Solve it graphically.
A chemical company produces two compounds, A and B. The following table gives the units of ingredients, C and D per kg of compounds A and B as well as minimum requirements of C and D and costs per kg of A and B. Find the quantities of A and B which would give a supply of C and D at a minimum cost.
| Compound | Minimum requirement | ||
| A | B | ||
| Ingredient C Ingredient D |
1 3 |
2 1 |
80 75 |
| Cost (in Rs) per kg | 4 | 6 | - |
A manufacturer of patent medicines is preparing a production plan on medicines, A and B. There are sufficient raw materials available to make 20000 bottles of A and 40000 bottles of B, but there are only 45000 bottles into which either of the medicines can be put. Further, it takes 3 hours to prepare enough material to fill 1000 bottles of A, it takes 1 hour to prepare enough material to fill 1000 bottles of B and there are 66 hours available for this operation. The profit is Rs 8 per bottle for A and Rs 7 per bottle for B. How should the manufacturer schedule his production in order to maximize his profit?
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp while it takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at most 20 hours and the grinding/cutting machine for at most 12 hours. The profit from the sale of a lamp is ₹5.00 and a shade is ₹3.00. Assuming that the manufacturer sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
A company manufactures two articles A and B. There are two departments through which these articles are processed: (i) assembly and (ii) finishing departments. The maximum capacity of the first department is 60 hours a week and that of other department is 48 hours per week. The product of each unit of article A requires 4 hours in assembly and 2 hours in finishing and that of each unit of B requires 2 hours in assembly and 4 hours in finishing. If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B, find the number of units of A and B to be produced per week in order to have maximum profit.
An oil company has two depots, A and B, with capacities of 7000 litres and 4000 litres respectively. The company is to supply oil to three petrol pumps, D, E, F whose requirements are 4500, 3000 and 3500 litres respectively. The distance (in km) between the depots and petrol pumps is given in the following table:
Figure
Assuming that the transportation cost per km is Rs 1.00 per litre, how should the delivery be scheduled in order that the transportation cost is minimum?
There are two types of fertilizers F1 and F2. F1 consists of 10% nitrogen and 6% phosphoric acid and F2 consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, a farmer finds the she needs atleast 14 kg of nitrogen and 14 kg of phosphoric acid for her crop. If F1 costs ₹6/kg and F2 costs ₹5/kg, determine how much of each type of fertilizer should be used so that the nutrient requirements are met at minimum cost. What is the minimum cost?
An aeroplane can carry a maximum of 200 passengers. A profit of ₹1000 is made on each executive class ticket and a profit of ₹600 is made on each economy class ticket. The airline reserves atleast 20 seats for executive class. However, atleast 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit of the airline. What is the maximum profit?
The region represented by the inequation system x, y ≥ 0, y ≤ 6, x + y ≤ 3 is
A carpenter has 90, 80 and 50 running feet respectively of teak wood, plywood and rosewood which is used to product A and product B. Each unit of product A requires 2, 1 and 1 running feet and each unit of product B requires 1, 2 and 1 running feet of teak wood, plywood and rosewood respectively. If product A is sold for Rs. 48 per unit and product B is sold for Rs. 40 per unit, how many units of product A and product B should be produced and sold by the carpenter, in order to obtain the maximum gross income? Formulate the above as a Linear Programming Problem and solve it, indicating clearly the feasible region in the graph.
A farmer has a supply of chemical fertilizer of type A which contains 10% nitrogen and 6% phosphoric acid and of type B which contains 5% nitrogen and 10% phosphoric acid. After the soil test, it is found that at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The fertilizer of type A costs ₹ 5.00 per kg and the type B costs ₹ 8.00 per kg. Using Linear programming, find how many kilograms of each type of fertilizer should be bought to meet the requirement and for the cost to be minimum. Find the feasible region in the graph.
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
The minimum value of z = 10x + 25y subject to 0 ≤ x ≤ 3, 0 ≤ y ≤ 3, x + y ≥ 5 is ______.
For the LPP, maximize z = x + 4y subject to the constraints x + 2y ≤ 2, x + 2y ≥ 8, x, y ≥ 0 ______.
The point which provides the solution to the linear programming problem: Max P = 2x + 3y subject to constraints: x ≥ 0, y ≥ 0, 2x + 2y ≤ 9, 2x + y ≤ 7, x + 2y ≤ 8, is ______
A feasible region in the set of points which satisfy ____________.
The maximum value of Z = 3x + 4y subjected to contraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0 and y ≥ 0 is ____________.
Which of the statements describe the solution set for `-2(x + 8) = - 2x + 20`?
Minimise z = – 3x + 4y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0 What will be the minimum value of z ?
Any point in the feasible region that gives the optional value (maximum or minimum) of the objective function is called:-
The maximum value of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
The shaded part of given figure indicates in feasible region, then the constraints are:
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
