Advertisements
Advertisements
Question
A factory uses three different resources for the manufacture of two different products, 20 units of the resources A, 12 units of B and 16 units of C being available. 1 unit of the first product requires 2, 2 and 4 units of the respective resources and 1 unit of the second product requires 4, 2 and 0 units of respective resources. It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Formulate the linear programming problem. How many units of each product should be manufactured for maximizing the profit? Solve it graphically.
Solution
Let x units of first product and y units of second product be manufactured.
Therefore, \[x, y \geq 0\]
The given information can be tabulated as follows:
| Product | Resource A | Resource B | Resource C |
| First(x) | 2 | 2 | 4 |
| Second(y) | 4 | 2 | 0 |
| Availability | 20 | 12 | 16 |
Therefore, the constraints are
\[2x + 4y \leq 20\]
\[2x + 2y \leq 12\]
\[4x + 0y \leq 16 \text{ or } 4x \leq 16\]
It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Therefore, profit gained from x units of first product and y units of second product is 2x monetary units and 4y monetary units respectively.
Total profit = Z = \[2x + 3y\] which is to be maximised
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = \[2x + 3y\]
subject to
\[2x + 4y \leq 20\]
\[2x + 2y \leq 12\]
\[4x + 0y \leq 16 \text { or} 4x \leq 16\]
\[x, y \geq 0\]
First we will convert inequations into equations as follows :
2x + 4y = 20, 2x + 2y = 12, 4x = 16, x = 0 and y = 0
Region represented by 2x + 4y ≤ 20:
The line 2x + 4y = 20 meets the coordinate axes at A1(10, 0) and B1(0, 5) respectively. By joining these points we obtain the line 2x + 4y = 20. Clearly (0,0) satisfies the 3x + 2y = 210. So,the region which contains the origin represents the solution set of the inequation 2x + 4y ≤ 20.
Region represented by 2x + 2y ≤ 12:
The line 2x +2y =16 meets the coordinate axes at C1(6, 0) and D1(0, 6) respectively. By joining these points we obtain the line 2x + 2y = 12. Clearly (0,0) satisfies the inequation 2x + 2y ≤ 12. So, the region which contains the origin represents the solution set of the inequation 2x + 2y ≤ 12.
Region represented by 4x ≤ 16:
The line 4x =16 or x = 4 is the line passing through the point E1(4, 0) and is parallel to Y axis.The region to the left of the line x = 4 would satisfy the inequation 4x ≤ 16.
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 2x + 4y ≤ 20, 2x + 2y ≤ 12, 4x ≤ 16, x ≥ 0 and y ≥ 0 are as follows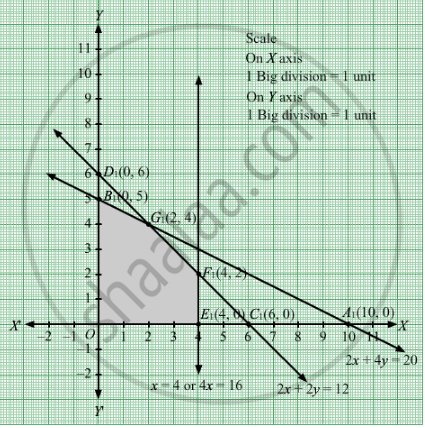
The corner points are O(0, 0), B1(0, 5), G1 \[\left( 2, 4 \right)\] F1(4, 2) and E1(4, 0).
The values of Z at these corner points are as follows
| Corner point | Z= 2x + 3y |
| O | 0 |
| B1 | 15 |
| G1 | 16 |
| F1 | 14 |
| E1 | 8 |
The maximum value of Z is 16 which is attained at G1 \[\left( 2, 4 \right)\] Thus, the maximum profit is 16 monetary units obtained when 2 units of first product and 4 units of second product were manufacture .
APPEARS IN
RELATED QUESTIONS
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
A dealer in rural area wishes to purchase a number of sewing machines. He has only Rs 5,760 to invest and has space for at most 20 items for storage. An electronic sewing machine cost him Rs 360 and a manually operated sewing machine Rs 240. He can sell an electronic sewing machine at a profit of Rs 22 and a manually operated sewing machine at a profit of Rs 18. Assuming that he can sell all the items that he can buy, how should he invest his money in order to maximize his profit? Make it as a LPP and solve it graphically.
A manufacturing company makes two types of teaching aids A and B of Mathematics for class XII. Each type of A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each type of B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available per week are 180 and 30, respectively. The company makes a profit of Rs 80 on each piece of type A and Rs 120 on each piece of type B. How many pieces of type A and type B should be manufactured per week to get maximum profit? Make it as an LPP and solve graphically. What is the maximum profit per week?
Solve the following L.P.P. graphically:
Minimise Z = 5x + 10y
Subject to x + 2y ≤ 120
Constraints x + y ≥ 60
x – 2y ≥ 0 and x, y ≥ 0
Solve the following L.P.P graphically: Maximise Z = 20x + 10y
Subject to the following constraints x + 2y ≤ 28,
3x + y ≤ 24,
x ≥ 2,
x, y ≥ 0
Maximise z = 8x + 9y subject to the constraints given below :
2x + 3y ≤ 6
3x − 2y ≤6
y ≤ 1
x, y ≥ 0
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 10x + 6y
Subject to
\[3x + y \leq 12\]
\[2x + 5y \leq 34\]
\[ x, y \geq 0\]
Maximize Z = x + y
Subject to
\[- 2x + y \leq 1\]
\[ x \leq 2\]
\[ x + y \leq 3\]
\[ x, y \geq 0\]
Maximize Z = 3x + 3y, if possible,
Subject to the constraints
\[x - y \leq 1\]
\[x + y \geq 3\]
\[ x, y \geq 0\]
Show the solution zone of the following inequalities on a graph paper:
\[5x + y \geq 10\]
\[ x + y \geq 6\]
\[x + 4y \geq 12\]
\[x \geq 0, y \geq 0\]
Find x and y for which 3x + 2y is minimum subject to these inequalities. Use a graphical method.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin contents of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs ₹16 and one kg of food Y costs ₹20. Find the least cost of the mixture which will produce the required diet?
Two tailors, A and B earn Rs 15 and Rs 20 per day respectively. A can stitch 6 shirts and 4 pants while B can stitch 10 shirts and 4 pants per day. How many days shall each work if it is desired to produce (at least) 60 shirts and 32 pants at a minimum labour cost?
A company produces two types of leather belts, say type A and B. Belt A is a superior quality and belt B is of a lower quality. Profits on each type of belt are Rs 2 and Rs 1.50 per belt, respectively. Each belt of type A requires twice as much time as required by a belt of type B. If all belts were of type B, the company could produce 1000 belts per day. But the supply of leather is sufficient only for 800 belts per day (both A and B combined). Belt A requires a fancy buckle and only 400 fancy buckles are available for this per day. For belt of type B, only 700 buckles are available per day.
How should the company manufacture the two types of belts in order to have a maximum overall profit?
A manufacturer makes two types A and B of tea-cups. Three machines are needed for the manufacture and the time in minutes required for each cup on the machines is given below:
| Machines | |||
| I | II | III | |
| A B |
12 6 |
18 0 |
6 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each cup A is 75 paise and that on each cup B is 50 paise, show that 15 tea-cups of type A and 30 of type B should be manufactured in a day to get the maximum profit.
A firm manufactures two products A and B. Each product is processed on two machines M1 and M2. Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2. The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs 3 and Rs 4 respectively.
Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp while it takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at most 20 hours and the grinding/cutting machine for at most 12 hours. The profit from the sale of a lamp is ₹5.00 and a shade is ₹3.00. Assuming that the manufacturer sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit?
A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2. Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
A manufacturer makes two products, A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 units of product A and 16 units of product B. A working week consists of 40 hours of production and the weekly turn over must not be less than Rs 10000. If the profit on each of product A is Rs 20 and an product B is Rs 30, then how many of each should be produced so that the profit is maximum? Also find the maximum profit.
A merchant plans to sell two types of personal computers a desktop model and a portable model that will cost Rs 25,000 and Rs 40,000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and his profit on the desktop model is Rs 4500 and on the portable model is Rs 5000. Make an LPP and solve it graphically.
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Types of Toys | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
A farmer has a supply of chemical fertilizer of type A which contains 10% nitrogen and 6% phosphoric acid and of type B which contains 5% nitrogen and 10% phosphoric acid. After the soil test, it is found that at least 7 kg of nitrogen and the same quantity of phosphoric acid is required for a good crop. The fertilizer of type A costs ₹ 5.00 per kg and the type B costs ₹ 8.00 per kg. Using Linear programming, find how many kilograms of each type of fertilizer should be bought to meet the requirement and for the cost to be minimum. Find the feasible region in the graph.
A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.
Find the graphical solution for the system of linear inequation 2x + y ≤ 2, x − y ≤ 1
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
The maximum value of Z = 5x + 4y, Subject to y ≤ 2x, x ≤ 2y, x + y ≤ 3, x ≥ 0, y ≥ 0 is ______.
For the function z = 19x + 9y to be maximum under the constraints 2x + 3y ≤ 134, x + 5y ≤ 200, x ≥ 0, y ≥ 0; the values of x and y are ______.
For the LPP, maximize z = x + 4y subject to the constraints x + 2y ≤ 2, x + 2y ≥ 8, x, y ≥ 0 ______.
A manufacturer wishes to produce two commodities A and B. The number of units of material, labour and equipment needed to produce one unit of each commodity is shown in the table given below. Also shown is the available number of units of each item, material, labour, and equipment.
| Items | Commodity A | Commodity B | Available no. of Units |
| Material | 1 | 2 | 8 |
| Labour | 3 | 2 | 12 |
| Equipment | 1 | 1 | 10 |
Find the maximum profit if each unit of commodity A earns a profit of ₹ 2 and each unit of B earns a profit of ₹ 3.
Which of the statements describe the solution set for `-2(x + 8) = - 2x + 20`?
Any point in the feasible region that gives the optional value (maximum or minimum) of the objective function is called:-
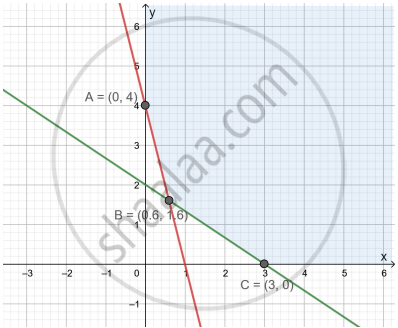
The corner points of the shaded unbounded feasible region of an LPP are (0, 4), (0.6, 1.6) and (3, 0) as shown in the figure. The minimum value of the objective function Z = 4x + 6y occurs at ______.
Solve the following linear programming problem graphically:
Minimize: Z = 5x + 10y
Subject to constraints:
x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
Solve the following Linear Programming Problem graphically:
Minimize: Z = 60x + 80y
Subject to constraints:
3x + 4y ≥ 8
5x + 2y ≥ 11
x, y ≥ 0
Solve the following Linear Programming Problem graphically:
Maximize: z = – x + 2y,
Subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
A linear programming problem is given by Z = px + qy where p, q > 0 subject to the constraints: x + y ≤ 60, 5x + y ≤ 100, x ≥ 0 and y ≥ 0
- Solve graphically to find the corner points of the feasible region.
- If Z = px + qy is maximum at (0, 60) and (10, 50), find the relation of p and q. Also mention the number of optimal solution(s) in this case.
