Advertisements
Advertisements
Question
A manufacturer makes two types A and B of tea-cups. Three machines are needed for the manufacture and the time in minutes required for each cup on the machines is given below:
| Machines | |||
| I | II | III | |
| A B |
12 6 |
18 0 |
6 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each cup A is 75 paise and that on each cup B is 50 paise, show that 15 tea-cups of type A and 30 of type B should be manufactured in a day to get the maximum profit.
Solution
Let x units of type A and y units of type B cups were made.
Quantities cannot be negative.Therefore, \[x, y \geq 0\]
As we are given,
| Machines | |||
| I | II | III | |
| A B |
12 6 |
18 0 |
6 9 |
Therefore, the constraints are
\[12x + 6y \leq 360\]
\[18x + 0y \leq 360\]
\[6x + 9y \leq 360\]
If the profit on each cup A is 75 paise and that on each cup B is 50 paise.
Total profit = Z = \[0 . 75x + 0 . 50y\] which is to be maximised.
Thus, the mathematical formulation of the given linear programmimg problem is
Max Z = \[0 . 75x + 0 . 50y\] subject to
\[12x + 6y \leq 360\]
\[18x + 0y \leq 360\]
\[6x + 9y \leq 360\]
First we will convert inequations into equations as follows :
12x + 6y = 360, 18x = 360,
Region represented by 12x + 6y ≤ 360:
The line 12x + 6y = 360 meets the coordinate axes at A1(30, 0) and B1(0, 60) respectively. By joining these points we obtain the line 12x + 6y = 360.Clearly (0,0) satisfies the 12x + 6y = 360. So,the region which contains the origin represents the solution set of the inequation 12x + 6y ≤ 360.
Region represented by 18x + 0y ≤ 360:
The line 18x + 0y = 360 meets the coordinate axes at C1(20, 0) . We obtain the line 18x + 0y = 360.Clearly (0,0) satisfies the inequation 18x + 0y ≤ 360. So,the region which contains the origin represents the solution set of the inequation 18x + 0y ≤ 360.
Region represented by
Region represented by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant satisfies these inequations. So, the first quadrant is the region represented by the inequations x ≥ 0, and y ≥ 0.
The feasible region determined by the system of constraints 12x + 6y ≤ 360, 18x + 0y ≤ 360,
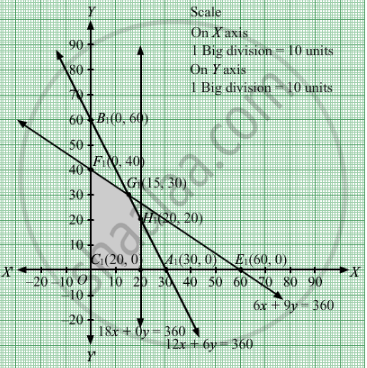
The values of Z at these corner points are as follows
| Corner point | Z= 0.75x + 0.50y |
| O | 0 |
| F1 | 20 |
| G1 | 26.25 |
| H1 | 25 |
| C1 | 15 |
Thus, the maximum profit is Rs 26.25 obtained when 15 units of type A and 30 units of type B cups were made.
APPEARS IN
RELATED QUESTIONS
Minimize : Z = 6x + 4y
Subject to the conditions:
3x + 2y ≥ 12,
x + y ≥ 5,
0 ≤ x ≤ 4,
0 ≤ y ≤ 4
A cooperative society of farmers has 50 hectares of land to grow two crops A and B. The profits from crops A and B per hectare are estimated as Rs 10,500 and Rs 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops A and B at the rate of 20 litres and 10 litres per hectare, respectively. Further not more than 800 litres of herbicide should be used in order to protect fish and wildlife using a pond which collects drainage from this land. Keeping in mind that the protection of fish and other wildlife is more important than earning profit, how much land should be allocated to each crop so as to maximize the total profit? Form an LPP from the above and solve it graphically. Do you agree with the message that the protection of wildlife is utmost necessary to preserve the balance in environment?
A manufacturer produces two products A and B. Both the products are processed on two different machines. The available capacity of first machine is 12 hours and that of second machine is 9 hours per day. Each unit of product A requires 3 hours on both machines and each unit of product B requires 2 hours on first machine and 1 hour on second machine. Each unit of product A is sold at Rs 7 profit and B at a profit of Rs 4. Find the production level per day for maximum profit graphically.
Solve the following L. P. P. graphically:Linear Programming
Minimize Z = 6x + 2y
Subject to
5x + 9y ≤ 90
x + y ≥ 4
y ≤ 8
x ≥ 0, y ≥ 0
Minimize Z = 18x + 10y
Subject to
\[4x + y \geq 20\]
\[2x + 3y \geq 30\]
\[ x, y \geq 0\]
Maximize Z = 3x + 5y
Subject to
\[x + 2y \leq 20\]
\[x + y \leq 15\]
\[ y \leq 5\]
\[ x, y \geq 0\]
Minimize Z = 3x1 + 5x2
Subject to
\[x_1 + 3 x_2 \geq 3\]
\[ x_1 + x_2 \geq 2\]
\[ x_1 , x_2 \geq 0\]
Maximize Z = 3x1 + 4x2, if possible,
Subject to the constraints
\[x_1 - x_2 \leq - 1\]
\[ - x_1 + x_2 \leq 0\]
\[ x_1 , x_2 \geq 0\]
A dietician mixes together two kinds of food in such a way that the mixture contains at least 6 units of vitamin A, 7 units of vitamin B, 11 units of vitamin C and 9 units of vitamin D. The vitamin contents of 1 kg of food X and 1 kg of food Y are given below:
| Vitamin A |
Vitamin B |
Vitamin |
Vitamin D |
|
| Food X Food Y |
1 2 |
1 1 |
1 3 |
2 1 |
One kg food X costs Rs 5, whereas one kg of food Y costs Rs 8. Find the least cost of the mixture which will produce the desired diet.
A wholesale dealer deals in two kinds, A and B (say) of mixture of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew nuts and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew nuts and 180 grams of hazel nuts. The remainder of both mixtures is per nuts. The dealer is contemplating to use mixtures A and B to make a bag which will contain at least 240 grams of almonds, 300 grams of cashew nuts and 540 grams of hazel nuts. Mixture A costs Rs 8 per kg. and mixture B costs Rs 12 per kg. Assuming that mixtures A and B are uniform, use graphical method to determine the number of kg. of each mixture which he should use to minimise the cost of the bag.
Reshma wishes to mix two types of food P and Q in such a way that the vitamin contents of the mixture contains at least 8 units of vitamin A and 11 units of vitamin B. Food P costs ₹60/kg and food Q costs ₹80/kg. Food P contains 3 units/kg of vitamin A and 5 units/kg of vitamin B while food Q contains 4 units/kg of vitamin A and 2 units/kg of vitamin B. Determine the minimum cost of the mixture.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing ₹250 per bag, contains 2 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing ₹200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
Two tailors, A and B earn Rs 15 and Rs 20 per day respectively. A can stitch 6 shirts and 4 pants while B can stitch 10 shirts and 4 pants per day. How many days shall each work if it is desired to produce (at least) 60 shirts and 32 pants at a minimum labour cost?
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requires 3 gm of silver and 1 gm of gold while that of type B requires 1 gm of silver and 2 gm of gold. The company can produce 9 gm of silver and 8 gm of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, find the number of units of each type that the company should produce to maximize the profit. What is the maximum profit?
A manufacturer of Furniture makes two products : chairs and tables. processing of these products is done on two machines A and B. A chair requires 2 hrs on machine A and 6 hrs on machine B. A table requires 4 hrs on machine A and 2 hrs on machine B. There are 16 hrs of time per day available on machine A and 30 hrs on machine B. Profit gained by the manufacturer from a chair and a table is Rs 3 and Rs 5 respectively. Find with the help of graph what should be the daily production of each of the two products so as to maximize his profit.
A firm manufactures two products A and B. Each product is processed on two machines M1 and M2. Product A requires 4 minutes of processing time on M1 and 8 min. on M2 ; product B requires 4 minutes on M1 and 4 min. on M2. The machine M1 is available for not more than 8 hrs 20 min. while machine M2 is available for 10 hrs. during any working day. The products A and B are sold at a profit of Rs 3 and Rs 4 respectively.
Formulate the problem as a linear programming problem and find how many products of each type should be produced by the firm each day in order to get maximum profit.
A factory uses three different resources for the manufacture of two different products, 20 units of the resources A, 12 units of B and 16 units of C being available. 1 unit of the first product requires 2, 2 and 4 units of the respective resources and 1 unit of the second product requires 4, 2 and 0 units of respective resources. It is known that the first product gives a profit of 2 monetary units per unit and the second 3. Formulate the linear programming problem. How many units of each product should be manufactured for maximizing the profit? Solve it graphically.
A firm manufactures headache pills in two sizes A and B. Size A contains 2 grains of aspirin, 5 grains of bicarbonate and 1 grain of codeine; size B contains 1 grain of aspirin, 8 grains of bicarbonate and 66 grains of codeine. It has been found by users that it requires at least 12 grains of aspirin, 7.4 grains of bicarbonate and 24 grains of codeine for providing immediate effects. Determine graphically the least number of pills a patient should have to get immediate relief. Determine also the quantity of codeine consumed by patient.
A company manufactures two types of novelty Souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours available for assembling. The profit is 50 paise each for type A and 60 paise each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats of first class. However, at least 4 times as many passengers prefer to travel by economy class to the first class. Determine how many each type of tickets must be sold in order to maximize the profit for the airline. What is the maximum profit.
Anil wants to invest at most Rs 12000 in Saving Certificates and National Saving Bonds. According to rules, he has to invest at least Rs 2000 in Saving Certificates and at least Rs 4000 in National Saving Bonds. If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bond is 10% per annum, how much money should he invest to earn maximum yearly income? Find also his maximum yearly income.
If a young man drives his vehicle at 25 km/hr, he has to spend ₹2 per km on petrol. If he drives it at a faster speed of 40 km/hr, the petrol cost increases to ₹5 per km. He has ₹100 to spend on petrol and travel within one hour. Express this as an LPP and solve the same.
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman's time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman's time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman's time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the number of tennis rackets and cricket bats that the factory must manufacture to earn the maximum profit. Make it as an LPP and solve it graphically.
A manufacturer considers that men and women workers are equally efficient and so he pays them at the same rate. He has 30 and 17 units of workers (male and female) and capital respectively, which he uses to produce two types of goods A and B. To produce one unit of A, 2 workers and 3 units of capital are required while 3 workers and 1 unit of capital is required to produce one unit of B. If A and B are priced at ₹100 and ₹120 per unit respectively, how should he use his resources to maximise the total revenue? Form the above as an LPP and solve graphically. Do you agree with this view of the manufacturer that men and women workers are equally efficient and so should be paid at the same rate?
There are two types of fertilisers 'A' and 'B' . 'A' consists of 12% nitrogen and 5% phosphoric acid whereas 'B' consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If 'A' costs ₹10 per kg and 'B' cost ₹8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requiremnets are met at a minimum cost
A medical company has factories at two places, A and B. From these places, supply is made to each of its three agencies situated at P, Q and R. The monthly requirements of the agencies are respectively 40, 40 and 50 packets of the medicines, while the production capacity of the factories, A and B, are 60 and 70 packets respectively. The transportation cost per packet from the factories to the agencies are given below:
| Transportation Cost per packet(in Rs.) | ||
| From-> | A | B |
| To | ||
| P | 5 | 4 |
| Q | 4 | 2 |
| R | 3 | 5 |
A company manufactures two types of products A and B. Each unit of A requires 3 grams of nickel and 1 gram of chromium, while each unit of B requires 1 gram of nickel and 2 grams of chromium. The firm can produce 9 grams of nickel and 8 grams of chromium. The profit is ₹ 40 on each unit of the product of type A and ₹ 50 on each unit of type B. How many units of each type should the company manufacture so as to earn a maximum profit? Use linear programming to find the solution.
Find the graphical solution for the system of linear inequation 2x + y ≤ 2, x − y ≤ 1
Maximum value of 4x + 13y subject to constraints x ≥ 0, y ≥ 0, x + y ≤ 5 and 3x + y ≤ 9 is ______.
The maximum of z = 5x + 2y, subject to the constraints x + y ≤ 7, x + 2y ≤ 10, x, y ≥ 0 is ______.
A feasible region in the set of points which satisfy ____________.
The corner points of the bounded feasible region of a LPP are A(0,50), B(20, 40), C(50, 100) and D(0, 200) and the objective function is Z = x + 2y. Then the maximum value is ____________.
Solve the following Linear Programming Problem graphically:
Maximize: P = 70x + 40y
Subject to: 3x + 2y ≤ 9,
3x + y ≤ 9,
x ≥ 0,y ≥ 0.
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.
Which of the following is not a constraint to the given Linear Programming Problem?
Solve the following Linear Programming Problem graphically.
Maximise Z = 5x + 2y subject to:
x – 2y ≤ 2,
3x + 2y ≤ 12,
– 3x + 2y ≤ 3,
x ≥ 0, y ≥ 0
Aman has ₹ 1500 to purchase rice and wheat for his grocery shop. Each sack of rice and wheat costs ₹ 180 and Rupee ₹ 120 respectively. He can store a maximum number of 10 bags in his shop. He will earn a profit of ₹ 11 per bag of rice and ₹ 9 per bag of wheat.
- Formulate a Linear Programming Problem to maximise Aman’s profit.
- Calculate the maximum profit.
